Question

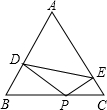
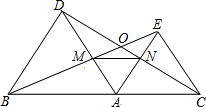
如图，点A是BC上一点，△ABD、△ACE都是等边三角形．
试说明：
（1）AM=AN；
（2）MN∥BC；
（3）∠DOM=60°．

Answer 1

证明：（1）∵△ABD、△ACE都是等边三角形，
∴AB=AD，AC=AE，∠BAD=∠CAE=60°，
∴180°-∠CAE=180°-∠BAD，
即∠BAE=∠DAC，
在△ABE和△ADC中，
∵

AB=AD ∠BAE=∠DAC AC=AE

，
∴△ABE≌△ADC（SAS），
∴∠ABE=∠ADC，
∵∠DAN=180°-∠BAD-∠CAE=180°-60°-60°=60°，
∴∠BAM=∠DAN，
在△ABM和△ADN中，
∵

∠ABE=∠ADC AB=AD ∠BAM=∠DAN

，
∴△ABM≌△ADN（ASA），
∴AM=AN；

（2）∵∠MAN=180°-60°×2=60°，AM=AN，
∴△AMN是等边三角形，
∴∠AMN=60°，
∴∠AMN=∠BAD，
∴MN∥BC；

（3）在△ABM中，∠AMB=180°-∠BAM-∠BAD，
在△DMO中，∠DMO=180°-∠DAN-∠DOM，
∵∠BAM=∠DAN（已证），∠AMB=∠DMO（对顶角相等），
∴∠DOM=∠BAD=60°．