题目内容

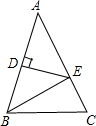
如图，△ABC中，∠C=90°，∠ABC的平分线交AC于点D，BC=6，AB=10，求CD的长．
如图，过点D作DE⊥AB于点E，∵∠C=90°，BD是∠ABC的平分线，
∴DE=CD，
∵BC=6，AB=10，
∴根据勾股定理得，AC=
AB2-BC2
=
102-62
=8，
设CD=x，则DE=x，
∵S△ABC=S△ABD+S△BCD，
∴
1
2
×6×8=
1
2
×6CD+
1
2
×10DE，
即24=3x+5x，
解得x=3，
即CD=3．
练习册系列答案
相关题目
在Rt△ABC中，已知∠C=90°，∠A=30°，BD是∠B的平分线，AC=18，则BD的值为（　　）
A．3
3
B．9C．12D．6
△ABC中，∠C=90°，AD平分∠BAC，BC=8，BD=5，则点D到AB的距离等于（　　）
A．5B．4C．3D．2
已知如图，∠B=∠C=90°，E是BC的中点，DE平分∠ADC，∠CED=35°，则∠EAB是______度．
如图，在△ABC中，∠C=90°，AD平分∠BAC，AC=12，CD=4，则点D到AB的距离为（　　）
A．3B．4C．6D．8
如图，∠AOB=30°，OC平分∠AOB，CD⊥OA于D，CE∥AO交OB于EOE=20cm，求CD的长．
如图，在Rt△ABC中，∠A=90°，BD平分∠ABC，交AC于点D，且AB=4，BD=5，那么点D到BC的距离是______．
如图，已知AB=AC，∠A=36°，AB的中垂线MN交AC于点D，交AB于点M，有下面4个结论：
①BD是∠ABC的角平分线；
②△BCD是等腰三角形；
③△ABC∽△BCD；
④△AMD≌△BCD．
（1）判断其中正确的结论是哪几个？
（2）从你认为是正确的结论中选一个加以证明．
如图，△ABC中，AB=AC，DE是AB的垂直平分线，D为垂足，交AC于E．
（1）若∠A=42°，求∠EBC的度数．
（2）若AB=10cm，△ABC的周长为27cm，求△BCE的周长．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网