题目内容
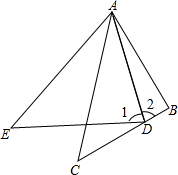
如图,已知AB=AC,∠A=36°,AB的中垂线MN交AC于点D,交AB于点M,有下面4个结论:
①BD是∠ABC的角平分线;
②△BCD是等腰三角形;
③△ABC∽△BCD;
④△AMD≌△BCD.
(1)判断其中正确的结论是哪几个?
(2)从你认为是正确的结论中选一个加以证明.

①BD是∠ABC的角平分线;
②△BCD是等腰三角形;
③△ABC∽△BCD;
④△AMD≌△BCD.
(1)判断其中正确的结论是哪几个?
(2)从你认为是正确的结论中选一个加以证明.

(1)连接BD,
①∵AB=AC,∠A=36°
∴△ABC是等腰三角形,∠ABC=∠ACB=
=72°,
∵AB垂直平分线交AC于D,交AB于M,
∴根据中垂线的性质,中垂线上的点到线段的两个端点的距离相等.
有AD=BD,∴∠A=∠ABD=36°,
∴∠DBC=∠ABC-∠ABD=72°-36°=36°,
∴BD平分∠ABC,故正确;
②∴∠BDC=180°-∠C-∠DBC=180°-72°-36°=72°,
∴BD=BC,
∴△BCD是等腰三角形.故正确;
③∠ABC=∠ACB=∠BDC=∠C,
∴△ABC∽△BCD,故正确;
④∵∠AMD=90°≠∠C=72°,
∴△AMD与△BCD不是全等三角形.故不正确.
∴①、②、③命题都正确.正确的结论是①、②、③;
(2)证明:BD平分∠ABC,
∵AB=AC,∠A=36°
∴△ABC是等腰三角形,∠ABC=∠ACB=
=72°,
∵AB垂直平分线交AC于D,交AB于M,
∴根据中垂线的性质,中垂线上的点到线段的两个端点的距离相等.有AD=BD,
∴∠A=∠ABD=36°,
∴∠DBC=∠ABC-∠ABD=72°-36°=36°,
∴BD平分∠ABC.
①∵AB=AC,∠A=36°
∴△ABC是等腰三角形,∠ABC=∠ACB=
| 180°-36° |
| 2 |
∵AB垂直平分线交AC于D,交AB于M,
∴根据中垂线的性质,中垂线上的点到线段的两个端点的距离相等.
有AD=BD,∴∠A=∠ABD=36°,
∴∠DBC=∠ABC-∠ABD=72°-36°=36°,
∴BD平分∠ABC,故正确;
②∴∠BDC=180°-∠C-∠DBC=180°-72°-36°=72°,
∴BD=BC,
∴△BCD是等腰三角形.故正确;
③∠ABC=∠ACB=∠BDC=∠C,
∴△ABC∽△BCD,故正确;
④∵∠AMD=90°≠∠C=72°,
∴△AMD与△BCD不是全等三角形.故不正确.
∴①、②、③命题都正确.正确的结论是①、②、③;
(2)证明:BD平分∠ABC,
∵AB=AC,∠A=36°
∴△ABC是等腰三角形,∠ABC=∠ACB=
| 180°-36° |
| 2 |
∵AB垂直平分线交AC于D,交AB于M,
∴根据中垂线的性质,中垂线上的点到线段的两个端点的距离相等.有AD=BD,
∴∠A=∠ABD=36°,
∴∠DBC=∠ABC-∠ABD=72°-36°=36°,
∴BD平分∠ABC.

练习册系列答案
相关题目