Question

【题目】如图，PA为⊙O的切线，A为切点，直线PO交⊙O于点E，F过点A作PO的垂线AB垂足为D，交⊙O于点B，延长BO与⊙O交与点C，连接AC，BF．

（1）求证：PB与⊙O相切；
（2）是探究线段EF，OD，OP之间的数量关系，并加以证明；
（3）若tan∠F= ，求cos∠ACB的值．

Answer 1

【答案】
（1）解：如图，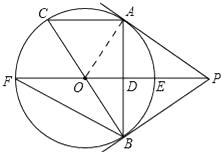

连接OA，
∵PD⊥AB，
∴OP垂直平分AB，
∴PA=PB，OA=OB，
∴△OAP≌△OBP，
∴∠OAP=∠OBP，
∵PA为⊙O的切线，
∴∠OAP=90°，
∴∠OQP=90°，
∵点B在⊙O上，
∴BP与⊙O相切
（2）解：EF，OD，OP间的数量关系为4EF2=OD×OP，
理由：∵∠OAP=90°，AD⊥OP，
∴OA2=OD×OP，
∵OA= EF，
∴OD×OP= EF2 ，
∴4EF2=OD×OP
（3）解：∵tanF= ，设BD=a，
∴FD=2a，AD=a，DE= a，EF= a，
∴OD= a，
∴AC= a，
∴cos∠ACB=
【解析】考查对圆的认识，正多边形和圆（内角，外角，中心角，边心距，边长，周长，面积的计算），弧长的计算 ，扇形面积的计算等考点的理解.
小题1 连接OA，利用垂径定理得到D为AB的中点，即OP垂直平分AB，利用SSS得出三角形AOP与三角形BOP全等，由PA为圆的切线，得到OA垂直于AP，利用全等三角形的对应角相等及垂直的定义得到OB垂直于BP，即PB为圆O的切线.
小题2 由一对直角相等，一对公共角，得出三角形AOD与三角形OAP相似，由相似得比例，列出关系式，由OA为EF的一半，等量代换即可得证.
小题3 根据勾股定理易求BC的长；最后由余弦三角函数的定义求解.