题目内容
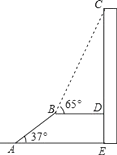
【题目】如图,AB是长为10m,倾斜角为37°的自动扶梯,平台BD与大楼CE垂直,且与扶梯AB的长度相等,在B处测得大楼顶部C的仰角为65°,求大楼CE的高度(结果保留整数).
(参考数据:sin37°≈ ![]() ,tan37°≈
,tan37°≈ ![]() ,sin65°≈
,sin65°≈ ![]() ,tan65°≈
,tan65°≈ ![]() )
)
【答案】解:过点B作BF⊥AE于点F.则BF=DE.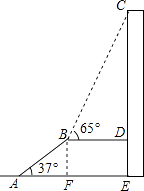
在Rt△ABF中,sin∠BAF= ![]() ∴BF=ABsin∠BAF=10×
∴BF=ABsin∠BAF=10× ![]() =6(m).
=6(m).
又在Rt△CDB中,tan∠CBD= ![]() ,∴CD=BDtan65°=10×
,∴CD=BDtan65°=10× ![]() ≈21(m)
≈21(m)
∴CE=DE+CD=BF+CD=6+21=27(m).
答:大楼CE的高度是27m
【解析】作BF⊥AE于点F.则BF=DE,在直角△ABF中利用三角函数求得BF的长,在直角△CDB中利用三角函数求得CD的长,则CE即可求得.
【考点精析】本题主要考查了关于仰角俯角问题的相关知识点,需要掌握仰角:视线在水平线上方的角;俯角:视线在水平线下方的角才能正确解答此题.

练习册系列答案
相关题目
【题目】一辆经营长途运输的货车在高速公路的A处加满油后,以每小时80千米的速度匀速行驶,前往B地,如表记录的是货车一次加满油后油箱内余油量y(升)与行驶时间x(时)之间的关系:
行驶时间x/时 | 0 | 1 | 2 | 2.5 |
余油量y/升 | 100 | 80 | 60 | 50 |
则y与x的函数关系式为_____,自变量x的取值范围为_____.