题目内容
【题目】如图:

(1)如图1,将长方形纸片ABFE沿着线段DC折叠,CF交AD于点H,过点H作HG∥DC,交线段CB于点G.
①判断∠FHG与∠EDC是否相等,并说明理由;
②说明HG平分∠AHC的理由.
(2)如图2,如果将(1)中的已知条件改为折叠三角形纸片ABE,其它条件不变.HG是否平分∠AHC?如果平分请说明理由;如果不平分,请找出∠CHG,∠AHG与∠E的数量关系并说明理由.
【答案】(1)①∠FHG=∠EDC,见解析;②见解析;(2)HG不再平分∠AHC,∠AHG=∠CHG+∠E,见解析.
【解析】
(1) ①根据平行线性质得∠EDA=∠FHA,∠ADC=∠AHG,由角的计算即可得证.
② HG平分∠AHC,理由如下:将图形折回到其原始状态,E的对应点为N,F的对应点为M,由折叠性质知:∠FCD=∠DCM,根据平行线性质得:∠DCM=∠HGC,∠DCH=∠CHG,∠CGH=∠AHG,等量代换得∠CHG=∠AHG,根据角平分线定义即可得证.
(2) HG不再平分∠AHC,∠AHG=∠CHG+∠E;理由如下:如图:延长线段AD和BC交于点F,根据平行线性质得:∠CHG=∠DCH=∠FCD,∠AHG=∠ADC,由三角形内角和定理、等量代换即可得证.
(1)①如图1,
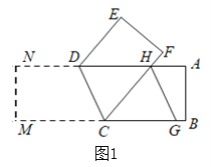
∵DE∥CF,
∴∠EDA=∠FHA(两直线平行,同位角相等),
∵HG∥DC,
∠ADC=∠AHG(两直线平行,同位角相等),
∴∠EDA +∠ADC=∠FHA +∠AHG,
∴∠FHG=∠EDC.
② HG平分∠AHC,理由如下:
将图形折回到其原始状态,E的对应点为N,F的对应点为M,
由折叠知∠FCD=∠DCM.
∵HG∥DC,
∴∠DCM=∠HGC(两直线平行,同位角相等),
∠DCH=∠CHG(两直线平行,内错角相等),
∵AD∥BC,
∴∠CGH=∠AHG(两直线平行,内错角相等),
∴∠CHG=∠AHG,
即HG平分∠AHC.
(2)HG不再平分∠AHC.∠AHG=∠CHG+∠E.
理由如下:
如图2,延长线段AD和BC交于点F,
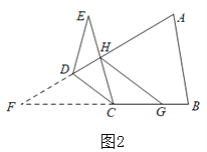
得到∠ECD=∠FCD.
∵HG∥DC,
∴∠CHG=∠DCH=∠FCD,
∠AHG=∠ADC,
∵∠ADC+∠FDC=180
又∵∠F+∠FCD+∠FDC=180
∴∠AHG=∠CHG+∠E

 阅读快车系列答案
阅读快车系列答案【题目】某服装店用10000元购进A,B两种新式服装,按标价售出后可获得毛利润5400元(毛利润=售价﹣进价),这两种服装的进价、标价如表所示:
类型、价格 | A型 | B型 |
进价(元/件) | 80 | 100 |
标价(元/件) | 120 | 160 |
(1)这两种服装各购进的件数;
(2)如果A种服装按标价的8折出售,要使这批服装全部售出后毛利润不低于2000元,则B种服装至多按标价的几折出售?



