Question

【题目】如图，反比例函数y= 的图象与二次函数y=﹣x2+bx+c的图象在第一象限内相交A、B两点，A、B两点的纵坐标分别为1，3，且AB=2

（1）求反比例函数的解析式；
（2）求二次函数的解析式；
（3）如果M为x轴上一点，N为y轴上一点，以点A，B，M，N为顶点的四边形是平行四边形，试求直线MN的函数表达式．

Answer 1

【答案】
（1）解：∵A、B两点都在反比例函数y= 的图象上，两点的纵坐标分别为1，3，
故可设A（x1 ， 1）B（x2 ， 3），分别代入反比例函数的解析式为k=x1 ， k=3x2 ，
解得x1=3x2 ，
由AB=2 ，
可得（x1﹣x2）2+（1﹣3）2=（2 ）2 ， x2=±2，
因为函数图象在第一象限，
故x2=2，k=3x2=6，
∴该反比例函数的解析式为：
y=
（2）由（1）可知，A（6，1），B（2，3），代入二次函数的解析式，
得 ，
解得 ，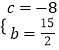
故此二次函数的解析式为：y=﹣x2+ x﹣8
（3）解：设M（x，0），N（0，y），过A、B两点的直线解析式为y=kx+b，
把A、B两点坐标代入得 ，
解得k=﹣ ．
则设经过M、N两点的直线解析式为y=﹣ x+b，
把M（x，0），N（0，y）代入得y=b，x=2b，
∵MN=AB，即x2+y2=（2 ）2 ， 即b2=4，b=±2，
故过M，N两点的直线解析式为：y=﹣ x+2或y=﹣ x﹣2
【解析】本题考查的是一次函数，反比例函数及二次函数图象上点的坐标特点，涉及面较广，但难度适中．
小题1 设出A、B两点的坐标，根据两点都在反比例函数的图象上，可找出两坐标之间的关系，由AB两点之间的距离可求出K的值，从而求出其解析式；
小题2 根据小题1中所求A，B两点的坐标，分别代入二次函数的解析式即可求出b、c的值，从而求出二次函数的解析式；
小题3 设出M，N两点的坐标，由A，B两点的坐标可求出过A，B两点直线的解析式，根据其解析式可设出过M，N两点的直线解析式，找出两点坐标与的关系，再根据平行四边形的性质即可求出未知数的值从而求出其解析式．