题目内容
【题目】阅读下列例题的解题过程,并完成相关问题
例:如图,在四边形ABCD中,AD∥BC,∠B=90°,AB=8 cm,AD=12cm,BC=18cm,点P从点A出发,以1cm/s的速度向点D运动;点Q从点C同时出发,以2cm/s的速度向点B运动.规定其中一个动点到达端点时,另一个动点也随之停止运动.从运动开始,使PQ∥CD和PQ=CD,分别经过多长时间?为什么?
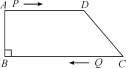
解:①设经过ts时,PQ∥CD且PQ=CD,此时四边形PQCD为平行四边形.
∵PD=(12-t)cm,CQ=2t cm,
∴12-t=2t.∴t=4.
∴当t=4时,PQ∥CD,且PQ=CD.
②设经过ts时,PQ=CD,分别过点P,D作BC边的垂线PE,DF,垂足分别为E,F.
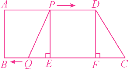
当CF=EQ时,四边形PQCD为梯形(腰相等)或者平行四边形.
∵∠B=∠A=∠DFB=90°,
∴四边形ABFD是矩形.∴AD=BF.
∵AD=12 cm,BC=18 cm,
∴CF=BC-BF=6 cm.
当四边形PQCD为梯形(腰相等)时,
PD+2(BC-AD)=CQ,
∴(12-t)+12=2t.∴t=8.
∴当t=8时,PQ=CD.
当四边形PQCD为平行四边形时,由①知当t=4时,PQ=CD.
综上,当t=4时,PQ∥CD;当t=4或t=8时,PQ=CD.
问题1:在整个运动过程中是否存在t值,使得四边形PQCD是菱形?若存在,请求出t值;若不存在,请说明理由.
问题2:从运动开始,当t取何值时,四边形PQBA是矩形?
问题3:在整个运动过程中是否存在t值,使得四边形PQBA是正方形?若存在,请求出t值;若不存在,请说明理由.
问题4:是否存在t,使得△DQC是等腰三角形?若存在,请求出t值;若不存在,请说明理由.
【答案】问题1:不存在.理由见解析;问题2:当t=6时,四边形PQBA是矩形;问题3:不存在.理由见解析;问题4:当t=5或6或![]() 时,△DQC是等腰三角形.
时,△DQC是等腰三角形.
【解析】
问题1:要使四边形PQCD是菱形,则四边形PQCD一定是平行四边形,由例可知当t=4时,四边形PQCD是平行四边形,而此时DP≠DC,从而可得出结论;
问题2:因为∠B=90°,AP∥BQ,由矩形的判定可知当AP=BQ时,四边形ABQP成为矩形,据此列方程求解即可;
问题3:要使四边形PQBA是正方形,则四边形PQBA一定是矩形.由问题2知当t=6时,四边形PQBA是矩形,而此时AP≠AB,从而可得出结论;
问题4:分三种情况讨论计算,①当QC=DC时;②当DQ=DC时,过点D作DH⊥CQ;③当QD=QC时,过点D作DH⊥CQ,分别列出方程求出时间,判断时间是否符合题意即可.
解:问题1:不存在.理由:
要使四边形PQCD是菱形,则四边形PQCD一定是平行四边形.
由例知当t=4时,四边形PQCD是平行四边形.
此时DP=12-t=8≠10,即DP≠DC,
所以按已知速度运动,四边形PQCD只能是平行四边形,但不可能是菱形.
问题2:如图,由题意,得AP=t,DP=12-t,CQ=2t,BQ=18-2t.
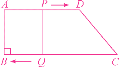
要使四边形PQBA是矩形,已有∠B=90°,AD∥BC,即AP∥BQ,只需满足AP=BQ,即t=18-2t,解得t=6.
所以当t=6时,四边形PQBA是矩形.
问题3:不存在.理由:
要使四边形PQBA是正方形,则四边形PQBA一定是矩形.
由问题2知当t=6时,四边形PQBA是矩形.
此时AP=t=6≠8,即AP≠AB,
所以按已知速度运动,四边形PQBA只能是矩形,但不可能是正方形.
问题4:当△DQC是等腰三角形时,分三种情况:
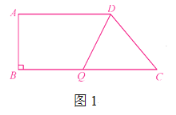
①如图1,当QC=DC时,即2t=10,∴t=5.
②如图2,当DQ=DC时,过点D作DH⊥CQ,
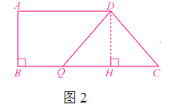
则QH=CH=![]() CQ=t.
CQ=t.
在Rt△DHC中,DH=8,CH=BC-AD=6,
∴DC=![]() =10,
=10,
∴t=6.
③如图3,当QD=QC时,过点D作DH⊥CQ,DH=8,CH=6,DC=10,CQ=QD=2t,QH=2t-6.
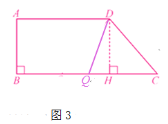
在Rt△DQH中,DH2+QH2=DQ2.
∴82+(2t-6)2=(2t)2.
解得t=![]() .
.
综上,当t=5或6或![]() 时,△DQC是等腰三角形.
时,△DQC是等腰三角形.