题目内容
【题目】在三角形△ABC中,D是BC边的中点,AD=![]() BC.
BC.
(1)△ABC的形状为 .
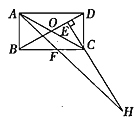
(2)如图,BM=3,BC=12,∠B=45°,∠MAN=45°,求CN;
(3)在(2)的条件下,AN= .

【答案】(1)直角三角形;(2)CN=4;(3)![]() .
.
【解析】
(1)已知BD=DC,AD=![]() BC,得DA=DB=DC,所以
BC,得DA=DB=DC,所以![]() ,又因为
,又因为![]() ,可得∠BAC=
,可得∠BAC=![]() ,所以△ABC为直角三角形.
,所以△ABC为直角三角形.
(2)设CN=x.ACB=∠B=45°,可得AB=AC.因为BD=DC,可得AD⊥BC,将△BAM绕点A逆时针旋转90°得到△ACH,连接NH.证明△NAM≌△NAH,可得MN=NH.根据NH2=CH2+CN2,列出方程(9﹣x)2=x2+32,解得CN=x=4
(3)在Rt△ADN中,∠ADN=90°,AD= 6,DN=2,利用勾股定理即可求得AN=![]()
(1)结论:△ABC是直角三角形.
理由:∵BD=DC,AD=![]() BC,
BC,
∴DA=DB=DC,
∴![]()
∵![]()
∴∠BAC=![]()
故答案为:直角三角形.
(2)如图,设CN=x.

∵∠B=45°,∠BAC=90°,
∴∠ACB=∠B=45°,
∴AB=AC.
∵BD=DC,
∴AD⊥BC,
将△BAM绕点A逆时针旋转90°得到△ACH,连接NH.
∵∠ACB=∠ACH=∠B=45°,
∴∠NCH=90°.
∵∠MAN=45°,∠MAH=90°,
∴∠NAM=∠NAH=45°.
∵NA=NA,AM=AH,
∴△NAM≌△NAH(SAS),
∴MN=NH.
∵BM=CH=3,BC=12,
∴CM=12﹣3=9,
∴MN=NH=9﹣x.
∵NH2=CH2+CN2,
∴(9﹣x)2=x2+32,
解得:x=4,
∴CN=4.
(3)在Rt△ADN中,
∵∠ADN=90°,AD=BD=CD=6,DN=CD﹣CN=6﹣4=2,
∴AN=![]()
故答案为:![]()

【题目】某校为了解2014年八年级学生课外书籍借阅情况,从中随机抽取了50名学生课外书籍借阅情况,将统计结果列出如下的表格,并绘制成如图所示的扇形统计图,其中科普类册数占这50名学生借阅总册数的40%.
类别 | 科普类 | 教辅类 | 文艺类 | 其他 |
册数(本) | 168 | 105 | m | 32 |
(1)表格中字母m的值等于 ;
(2)扇形统计图中“教辅类”所对应的圆心角α的度数为 °;
(3)该校2014年八年级有600名学生,请你估计该年级学生共借阅教辅类书籍约多少本?