题目内容
【题目】如图,已知矩形 ![]() 的边长
的边长 ![]() .某一时刻,动点
.某一时刻,动点 ![]() 从
从 ![]() 点出发沿
点出发沿 ![]() 方向以
方向以 ![]() 的速度向
的速度向 ![]() 点匀速运动;同时,动点
点匀速运动;同时,动点 ![]() 从
从 ![]() 点出发沿
点出发沿 ![]() 方向以
方向以 ![]() 的速度向
的速度向 ![]() 点匀速运动,问:
点匀速运动,问: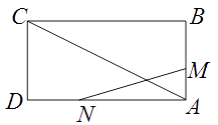
(1)经过多少时间, ![]() 的面积等于矩形
的面积等于矩形 ![]() 面积的
面积的 ![]() ?
?
(2)是否存在时刻t,使以A,M,N为顶点的三角形与 ![]() 相似?若存在,求t的值;若不存在,请说明理由.
相似?若存在,求t的值;若不存在,请说明理由.
【答案】
(1)解:设经过 ![]() 秒后,
秒后, ![]() 的面积等于矩形
的面积等于矩形 ![]() 面积的
面积的 ![]() ,
,
则有: ![]() ,即
,即 ![]() ,
,
解方程,得 ![]() .
.
经检验,可知 ![]() 符合题意,所以经过1秒或2秒后,
符合题意,所以经过1秒或2秒后, ![]() 的面积等于矩形
的面积等于矩形 ![]() 面积的
面积的 ![]()
(2)解:假设经过 ![]() 秒时,以
秒时,以 ![]() 为顶点的三角形与
为顶点的三角形与 ![]() 相似,
相似,
由矩形 ![]() ,可得
,可得 ![]() ,
,
因此有 ![]() 或
或 ![]()
即 ![]() ①,或
①,或 ![]() ②.
②.
解①,得 ![]() ;解②,得
;解②,得 ![]()
经检验, ![]() 或
或 ![]() 都符合题意,所以动点
都符合题意,所以动点 ![]() 同时出发后,经过
同时出发后,经过 ![]() 秒或
秒或 ![]() 秒时,以
秒时,以 ![]() 为顶点的三角形与
为顶点的三角形与 ![]() 相似
相似
【解析】(1)根据△AMN的面积等于矩形ABCD面积的![]() ,得到一元二次方程,求出它的解,求出时间;(2)根据相似三角形的判定方法,两边对应成比例且夹角相等,两三角形相似;求出t的值;此题是综合题,难度较大,计算和解方程时需认真仔细.
,得到一元二次方程,求出它的解,求出时间;(2)根据相似三角形的判定方法,两边对应成比例且夹角相等,两三角形相似;求出t的值;此题是综合题,难度较大,计算和解方程时需认真仔细.

练习册系列答案
相关题目