题目内容
【题目】已知:抛物线y=x2+bx+c经过点(2,-3)和(4,5).
(1)求抛物线的表达式及顶点坐标;
(2)将抛物线沿x轴翻折,得到图象G,求图象G的表达式;
(3)在(2)的条件下,当-2<x<2时,直线y=m与该图象有一个公共点,求m的值或取值范围.
【答案】
(1)解:解:把(2,-3)和(4,5)分别代入y=x+bx+c
得: ![]() ,解得:
,解得: ![]() ,
,
∴抛物线的表达式为:y=x-2x-3.
∵y=x-2x-3=(x-1)2-4.
∴顶点坐标为(1,-4)
(2)解:∵将抛物线沿x轴翻折,
得到图象G与原抛物线图形关于x轴对称,
∴图像G的表达式为:y=-x+2x+3
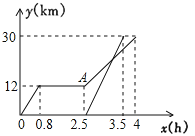
(3)解:如图,
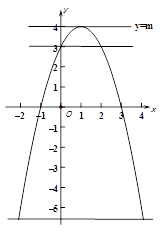
当0≤x<2时,y=m过抛物线顶点(1,4)时,
直线y=m与该图象有一个公共点,
此时y=4,∴m=4.
当-2<x<0时,直线y=m与该图象有一个公共点,
当y=m过抛物线上的点(0,3)时, y=3,∴m=3.
当y=m过抛物线上的点(-2,-5)时, y=-5,∴m=-5.
∴-5<m<3.
综上:m的值为4,或-5<m≤3.
【解析】(1)用待定系数法把(2,-3)和(4,5)分别代入y=x+bx+c,求出抛物线的表达式,根据顶点式得到顶点坐标;(2)根据抛物线沿x轴翻折,得到图象G与原抛物线图形关于x轴对称,得到图像G的表达式;(3)根据题意当0≤x<2时,y=m过抛物线顶点(1,4)时,直线y=m与该图象有一个公共点,求出y、m的值;当-2<x<0时,直线y=m与该图象有一个公共点,当y=m过抛物线上的点(0,3)时,求出y、m的值;当y=m过抛物线上的点(-2,-5)时,得到-5<m<3;求出m的值或取值范围.

【题目】父亲告诉小明:“距离地面越高,温度越低,”并给小明出示了下面的表格。
距离地面高度(千米) | 0 | 1 | 2 | 3 | 4 | 5 |
温度(℃) | 20 | 14 | 8 | 2 |
|
|
根据上表,父亲还给小明出了下面几个问题,你和小明一起回答。
(1)上表反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?
(2)如果用h表示距离地面的高度,用t表示温度,那么随着h的变化,t是怎么变化的?
(3)你能猜出距离地面6千米的高空温度是多少吗?