��Ŀ����
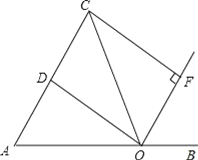
����Ŀ����ƽ��ֱ������ϵ�У�OΪԭ�㣬��B��x����������ϣ�D��0��8����������OBCD�۵���ʹ�ö���B����CD���ϵ�P�㴦��
��1����ͼ�٣���֪�ۺ����BC���ڵ�A����OD=2CP�����A�����꣮
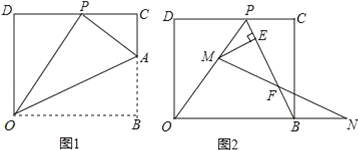
��2����ͼ���еĵ� P ǡ����CD�ߵ��е㣬���AOB�Ķ�����
��3����ͼ�ڣ��ڣ�I���������£���ȥ�ۺ�AO���߶�AP������BP������M���߶�OP�ϣ���M��P��O���غϣ�������N���߶�OB���ӳ����ϣ���BN=PM������MN��PB�ڵ�F����ME��BP�ڵ�E�����ʵ���M��N���ƶ������У��߶�EF�ij����Ƿ����仯�����仯��˵�����ɣ������䣬����߶�EF�ij��ȣ�ֱ��д��������ɣ�.
���𰸡���1��A��10��5������2����AOB=30�㣻��3���߶�EF�ij��Ȳ��䣬���ij���Ϊ2![]() ��
��
�������������������1����OB=OP=DC=x����DP=x��4����Rt��ODP�У�����OD2+DP2=OP2����ã�x=10��Ȼ����ݡ�ODP�ס�PCA�õ�AC=![]() =3���Ӷ��õ�AB=5����ʾ����A��10��5����
=3���Ӷ��õ�AB=5����ʾ����A��10��5����
��2�����ݵ�Pǡ����CD�ߵ��е���DP=PC=y����DC=OB=OP=2y����Rt��ODP�У�����OD2+DP2=OP2����ã�y=![]() ��Ȼ�����á�ODP�ס�PCA�õ�AC=
��Ȼ�����á�ODP�ס�PCA�õ�AC=![]() ���Ӷ�����tan��AOB=
���Ӷ�����tan��AOB=![]() �õ���AOB=30�㣻
�õ���AOB=30�㣻
��3����MQ��AN����PB�ڵ�Q�����MP=MQ��BN=QM���ó�MP=MQ������ME��PQ���ó�EQ=![]() PQ�����ݡ�QMF=��BNF��֤����MFQ�ա�NFB���ó�QF=
PQ�����ݡ�QMF=��BNF��֤����MFQ�ա�NFB���ó�QF=![]() QB�������EF=
QB�������EF=![]() PB���ɣ�1���еĽ������PB��������EF=
PB���ɣ�1���еĽ������PB��������EF=![]() PB���ɵó��߶�EF�ij��Ȳ��䣮
PB���ɵó��߶�EF�ij��Ȳ��䣮
�����������1����D��0��8������OD=BC=8��
��OD=2CP����CP=4��
��OB=OP=DC=x����DP=x��4��
��Rt��ODP�У�OD2+DP2=OP2������82+��x��4��2=x2����ã�x=10��
�ߡ�OPA=��B=90�㣬���ODP�ס�PCA����OD��PC=DP��CA��
��8��4=��x��4����AC����AC=![]() =3��
=3��
��AB=5��
���A��10��5����
��2���ߵ� P ǡ����CD�ߵ��е㣬
��DP=PC=y����DC=OB=OP=2y��
��Rt��ODP�У�OD2+DP2=OP2������82+y2=��2y��2����ã�y=![]() ��
��
�ߡ�OPA=��B=90�㣬���ODP�ס�PCA����OD��PC=DP��CA����8��y=y��AC��
��AC=![]() ����AB=8��
����AB=8��![]() =
=![]() ��
��
��OB=2y=![]() ����tan��AOB=
����tan��AOB=![]() =
=![]() =
=![]() ��
��
���AOB=30�㣻
��3����MQ��AN����PB�ڵ�Q����ͼ2��
��AP=AB��MQ��AN�����APB=��ABP=��MQP����MP=MQ��
��BN=PM����BN=QM��
��MP=MQ��ME��PQ����EQ=![]() PQ��
PQ��
��MQ��AN�����QMF=��BNF��
�ڡ�MFQ�͡�NFB�У� 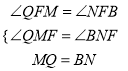 �����MFQ�ա�NFB��AAS����
�����MFQ�ա�NFB��AAS����
��QF=![]() QB��
QB��
��EF=EQ+QF=![]() PQ+
PQ+![]() QB=
QB=![]() PB��
PB��
�ɣ�1���еĽ��ۿɵã�PC=4��BC=8����C=90�㣬
��PB=![]() =4
=4![]() ��
��
��EF=![]() PB=2
PB=2![]() ��
��
���ڣ�1���������£�����M��N���ƶ������У��߶�EF�ij��Ȳ��䣬���ij���Ϊ2![]() ��
��