题目内容
【题目】如图,点O是线段AB上的一点,OA=OC,OD平分∠AOC交AC于点D,OF平分∠COB,CF⊥OF于点F.
(1)求证:四边形CDOF是矩形;
(2)当∠AOC多少度时,四边形CDOF是正方形?并说明理由.
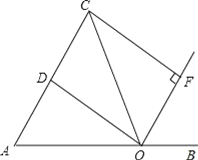
【答案】(1)证明见解析(2)当∠AOC=90°时,四边形CDOF是正方形,理由见解析
【解析】(1)证明:∵OD平分∠AOC,OF平分∠COB(已知),
∴∠AOC=2∠COD,∠COB=2∠COF。
∵∠AOC+∠BOC=180°,∴2∠COD+2∠COF=180°。∴∠COD+∠COF=90°。
∴∠DOF=90°。
∵OA=OC,OD平分∠AOC(已知)。
∴OD⊥AC,AD=DC(等腰三角形的“三合一”的性质)。∴∠CDO=90°。
∵CF⊥OF,∴∠CFO=90°。
∴四边形CDOF是矩形。
(2)解:当∠AOC=90°时,四边形CDOF是正方形。理由如下:
∵∠AOC=90°,AD=DC,∴OD=DC。
又由(1)知四边形CDOF是矩形,则四边形CDOF是正方形。
因此,当∠AOC=90°时,四边形CDOF是正方形。
(1)利用角平分线的性质、平角的定义可以求得∠DOF=90°;由等腰三角形的“三合一”的性质可推知OD⊥AC,即∠CDO=90°;根据已知条件“CF⊥OF”知∠CFO=90°;则三个角都是直角的四边形是矩形。
(2)当∠AOC=90°时,四边形CDOF是正方形;因为Rt△AOC的斜边上的中线OD等于斜边的一半,所以矩形的邻边OD=CD,所以矩形CDOF是正方形。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目