题目内容
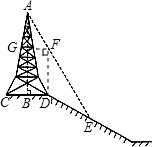
如图,在斜坡的顶部有一铁塔AB,B是CD的中点,CD是水平的,在阳光的照射下,塔影DE留在坡面上.已知铁塔底座宽CD=12m,塔影长DE=18m,小明和小华的身高都是1.6m,同一时刻,小明站在点E处,影子在坡面上,小华站在平地上,影子在平地上,两人的影长分别为2m和1m,求塔高AB.


过D作DF⊥CD,交AE于点F,过F作FG⊥AB,垂足为G.
由题意得:
=
.
∴DF=DE×1.6÷2=14.4(m).
∴GF=BD=
CD=6m.
又∵
=
.
∴AG=1.6×6=9.6(m).
∴AB=14.4+9.6=24(m).
答:铁塔的高度为24m
由题意得:
| DF |
| DE |
| 1.6 |
| 2 |
∴DF=DE×1.6÷2=14.4(m).
∴GF=BD=
| 1 |
| 2 |
又∵
| AG |
| GF |
| 1.6 |
| 1 |
∴AG=1.6×6=9.6(m).
∴AB=14.4+9.6=24(m).
答:铁塔的高度为24m


练习册系列答案
相关题目




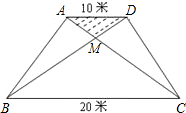 带种满花后,已经花了500元,请你预算一下,若继续在△BMC地带种植同样的太阳花,资金是否够用?并说明理由.
带种满花后,已经花了500元,请你预算一下,若继续在△BMC地带种植同样的太阳花,资金是否够用?并说明理由.