��Ŀ����
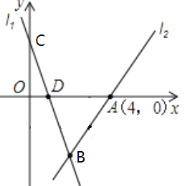
����Ŀ����ͼ��ֱ��l1��y=��3x+3��y����C����x�ύ�ڵ�D��ֱ��l2������A(4,0)����ֱ��l1��l2���ڵ�B(2,m����
��1����m��ֵ��ֱ��l2�ĺ�������ʽ��
��2��ֱ��l2�ڵ�һ�����ڵIJ�������һ��E���ҡ�ADE������ǡ�ADB�����һ�룬�����E�����꣬����x������һ��P��ʹ��CP+PE��ֵ��С����������Сֵ��
��3������QΪy����һ�㣬�ҡ�BDQΪ���������Σ���ֱ��д����Q�����ꣻ
���𰸡���1��m=-3��![]() ����2��E��5,1.5����
����2��E��5,1.5����![]() ����3��Q������Ϊ
����3��Q������Ϊ![]()
��������
��1������B(2,m������y=��3x+3��![]() m=
m=![]() ,�������ֱ��l2Ϊ
,�������ֱ��l2Ϊ![]()
��2�������D��1,0��,![]()
![]() ,��E������Ϊ
,��E������Ϊ![]() ��������ADE���������ADB�����һ�룬�������E��5,1.5�������ݶԳ�����������ͼ���ҵ�C����x��ĶԳƵ�C��,��ʱCP+PE=C,E��������֮����빫ʽ���������СֵΪC,E�ij�,
��������ADE���������ADB�����һ�룬�������E��5,1.5�������ݶԳ�����������ͼ���ҵ�C����x��ĶԳƵ�C��,��ʱCP+PE=C,E��������֮����빫ʽ���������СֵΪC,E�ij�,
��3���ֱ���B,DΪԲ��,BD��Ϊ�뾶����,�������y���ཻ��4������,�����BD���д�����y��Ľ���,�������������������ĵ�.
��1��![]() ��B(2,m����ֱ��l1��y=��3x+3�ϣ�
��B(2,m����ֱ��l1��y=��3x+3�ϣ�
![]() m=
m=![]()
��ֱ��l2�Ľ���ʽΪy=Kx+b
ֱ��l2������A(4,0)����B(2,-3����
![]()
![]()
���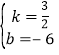
![]() ֱ��l2�Ľ���ʽΪ
ֱ��l2�Ľ���ʽΪ![]()
��2����y=0ʱ��0=-3x+3��x=1
![]() D��1,0��
D��1,0��
![]()
![]() ,
,
��E������Ϊ![]() ��
��
��![]()
a=5
![]() E��5,1.5��
E��5,1.5��
��C����x��ĶԳƵ�C��(0,-3),����C��E����x����P�㣬����CP������ͼ,
��ʱCP+EP����Сֵ����СֵΪC,E�ij�
![]()
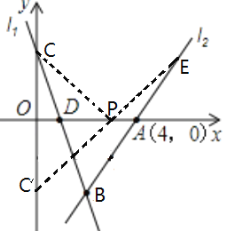
��3��Q������Ϊ![]()

 ��������ܸ�ϰϵ�д�
��������ܸ�ϰϵ�д�