题目内容
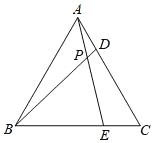
【题目】如图所示,正方形 ABCD 的面积为 16,△ABE 是等边三角形,点 E 在正方形 ABCD 内,在对角线 AC 上有一点 P,使 PD+PE 的和最小,则这个最小值为_____________ .

【答案】4
【解析】
先求得正方形的边长,依据等边三角形的定义可知 BE=AB=4,连结
BP,依据正方形的对称性可知 PB=PD,则 PE+PD=PE+BP.由两点之间线段最短可知:当点 B、P、E 在一条直线上时,PE+PD 有最小值,最小值为BE的长.
解:连结 BP.
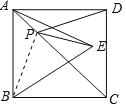
∵四边形 ABCD 为正方形,面积为 16,
∴正方形的边长为 4.
∵△ABE 为等边三角形,
∴BE=AB=4.
∵四边形 ABCD 为正方形,
∴△ABP 与△ADP 关于 AC 对称.
∴BP=DP.
∴PE+PD=PE+BP.
由两点之间线段最短可知:当点 B、P、E 在一条直线上时,PE+PD 有最小值, 最小值=BE=4.
故答案为:4.

练习册系列答案
相关题目
【题目】某校合唱团有30名成员,下表是合唱团成员的年龄分布统计表:
年龄(单位:岁) | 13 | 14 | 15 | 16 |
频数(单位:名) | 5 | 15 | x | 10﹣x |
对于不同的x,下列关于年龄的统计量不会发生改变的是( )
A.平均数、中位数
B.平均数、方差
C.众数、中位数
D.众数、方差