Question

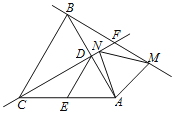
【题目】如图，等边△ABC中，边长为6，D、E分别是AB、AC的中点，连接DE，将△ADE绕点A顺时针旋转得到△AMN，其中D、E的对应点分别是M、N，直线BM与直线CN交于点F，若旋转360°，则点F经过的路径长是（　　）

A.B.8C.D.4

Answer 1

【答案】A

【解析】

设AB交CF于K．首先证明点F在弧上运动，∠GOK＝120°，当旋转360°，则点F经过的路径长是的两倍，求出的长度，即可求得答案．

如图，设AB交CF于K．

∵D、E分别是AB、AC的中点，

∴（三角形中位线定理），，，

∵△ABC是等边三角形，

∴，

∴△ADE是等边三角形，

由旋转得：，

∴∠CAB＝∠MAN＝60°，AB＝AC，AM＝AN，

∴∠CAN＝∠BAM，

∴△CAN≌△BAM（SAS），

∴∠ACN＝∠ABM，

∵∠CKA＝∠BKF，

∴∠BFK＝∠CAK＝60°，

∵∠CFB＝∠CAB＝60°，

∴C，B，F，A四点共圆，设圆心为O，

则点F在弧上运动，∠GOK＝120°，

∵等边△ABC的边长为6，

∵E是AC的中点，

∴，，

连接OA，则，

设圆的半径为r，

则的长为：，

当旋转360°，则点F经过的路径长是的两倍，

∴点F经过的路径长＝2×＝π，

故选：A．