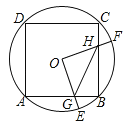
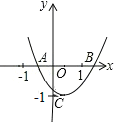
[题目]如图.已知二次函数的图象与轴分别交于.两点.与轴交于点.．则由抛物线的特征写出如下结论:①,②,③,④．其中正确的个数是()A. 4个B. 3个C. 2个D. 1个题目和参考答案——青夏教育精英家教网—

题目内容

【题目】如图，已知二次函数的图象与轴分别交于、两点，与轴交于点，．则由抛物线的特征写出如下结论：①；②；③；④．其中正确的个数是（）

A. 4个B. 3个C. 2个D. 1个

【答案】B

【解析】

根据抛物线的开口方向、对称轴的位置、图象与y轴的交点可分别确定a、b、c的符号，进而可判断①；

根据抛物线与x轴的交点的个数可判断②；

根据当时对应的函数值并结合图象可判断③；

设，则，把点A的坐标代入解析式即可判断④．

解：①观察图象可知，开口向上可得，对称轴在y轴右侧可得，与轴交于负半轴可得，∴，故①正确；

②∵抛物线与轴有两个交点，∴，即，故②错误；

③当时，由图象知在第二象限，∴，故③正确；

④设，则，∵，∴，把点A代入抛物线得，又，∴，故④正确；

所以正确的结论有①③④三个，故选：B．

练习册系列答案

如图（1）在△中，，底角的邻对记作，这时，容易知道一个角的大小与这个角的邻对值也是一一对应的．根据上述角的邻对的定义解下列问题：

（1）= ；

（2）如图（2），在△中，，，，求△的周长

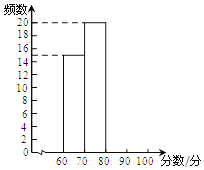
【题目】某学校组织七年级学生进行“垃圾分类”知识测试，现随机抽取部分学生的成绩进行统计，并绘制如下频数分布表以及频数分布直方图．

分数档	分数段/分	频数	频率
A	90＜x≤100	a	0.12
B	80＜x≤90	b	0.18
C	70＜x≤80	20	c
D	60＜x≤70	15	d

请根据以上信息，解答下列问题：

（1）已知A，B档的学生人数之和等于D档学生人数，求被抽取的学生人数，并把频数分布直方图补充完整．

（2）该校七年级共有200名学生参加测试，请估计七年级成绩在C档的学生人数．

（3）你能确定被抽取的这些学生的成绩的众数在哪一档吗？请说明理由．

【题目】如图，Rt△ABC中，∠ACB＝90°，AC＝6cm，BC＝8cm，动点P从点B出发，在BA边上以每秒5cm的速度向点A匀速运动，同时动点Q从点C出发，在CB边上以每秒4cm的速度向点B匀速运动，运动时间为t秒（0＜t＜2），连接PQ．

（1）若△BPQ与△ABC相似，求t的值；

（2）试探究t为何值时，△BPQ的面积是cm2；

（3）直接写出t为何值时，△BPQ是等腰三角形；

（4）连接AQ，CP，若AQ⊥CP，直接写出t的值．

【题目】如图，平面直角坐标系xOy中，A（2，1），B（3，﹣1），C（﹣2，1），D（0，2）．已知线段AB绕着点P逆时针旋转得到线段CD，其中C是点A的对应点．

（1）用尺规作图的方法确定旋转中心P，并直接写出点P的坐标；（要求保留作图痕迹，不写作法）

（2）若以P为圆心的圆与直线CD相切，求⊙P的半径

【题目】（2016湖北省咸宁市）如图，边长为4的正方形ABCD内接于点O，点E是上的一动点（不与A、B重合），点F是上的一点，连接OE、OF，分别与AB、BC交于点G，H，且∠EOF=90°，有以下结论：

①；

②△OGH是等腰三角形；

③四边形OGBH的面积随着点E位置的变化而变化；

④△GBH周长的最小值为．

其中正确的是________（把你认为正确结论的序号都填上）．

【题目】如图，抛物线与直线交于A、B两点.点A的横坐标为－3，点B在y轴上，点P是y轴左侧抛物线上的一动点，横坐标为m，过点P作PC⊥x轴于C，交直线AB于D.

（1）求抛物线的解析式；

（2）当m为何值时，；

（3）是否存在点P,使△PAD是直角三角形，若存在，求出点P的坐标；若不存在，说明理由.

【题目】如图，抛物线经过点，交y 轴于点C：

（1）求抛物线的顶点坐标．

（2）点为抛物线上一点，是否存在点使，若存在请直接给出点坐标；若不存在请说明理由．

（3）将直线绕点顺时针旋转，与抛物线交于另一点，求直线的解析式．

【题目】为加快城乡对接，建设美丽乡村，某地区对A、B两地间的公路进行改建，如图，A，B两地之间有一座山．汽车原来从A地到B地需途经C地沿折线ACB行驶，现开通隧道后，汽车可直接沿直线AB行驶，已知BC＝80千米，∠A＝45°，∠B＝30°．

(1)开通隧道前，汽车从A地到B地要走多少千米？

(2)开通隧道后，汽车从A地到B地可以少走多少千米？(结果保留根号)

试题分类