Question

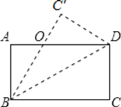
【题目】如图，点E、F、G、H分别是任意四边形ABCD中AD、BD、BC、CA的中点，
（1）求证：四边形EFGH是平行四边形；
（2）四边形ABCD的边至少满足什么条件时，四边形EFGH是菱形？并说明理由．

Answer 1

【答案】
（1）解：∵E，F是AD，DB中点，

∴EF∥AB，EF= AB，

∵H，G是AC，BC中点，

∴HG∥AB，HG= AB，

∴EF∥HG，EF=HG，

∴四边形EFGH是平行四边形，

（2）解：需添加条件AB=CD．

∵E，H是AD，AC中点，

∴EH= CD，

∵AB=CD，

∴EF=EH，

∴四边形EFGH是菱形．

【解析】（1）首先利用三角形的中位线定理证出EF∥AB，EF= AB，HG∥AB，HG= AB，可得四边形EFGH是平行四边形；（2）根据邻边相等的平行四边形是菱形，添加条件AB=CD后，证明EF=EH即可．