Question

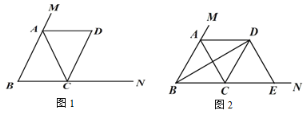
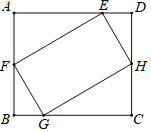
【题目】如图，矩形的四个顶点分别在矩形的各条边上，，，．有以下四个结论：①；②；③；④矩形的面积是．其中正确的结论为（ ）

A.①②B.①②③C.①②④D.①②③④

Answer 1

【答案】C

【解析】

根据矩形的性质和余角的性质可判定①；根据AAS可判定△BFG≌△DHE，即可判定②，证明△BFG∽△CGH，设GH=EF=a，得出BF，AF，CH，利用勾股定理求出a值，得到BF，再利用勾股定理求出BG=1，可得tan∠BFG，可判定③，计算出矩形EFGH的面积，可判定④.

解：∵∠FGH=90°，

∴∠BGF+∠CGH=90°，
又∵∠CGH+∠CHG=90°，
∴∠BGF=∠CHG，故①正确；
同理可得∠DEH=∠CHG，
∴∠BGF=∠DEH，
又∵∠B=∠D=90°，FG=EH，

在△BFG和△DHE中，

，
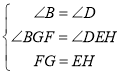∴△BFG≌△DHE（AAS），故②正确；
同理可得△AFE≌△CHG，
∴AF=CH，

由∠BGF=∠CHG，∠B=∠C=90°，
可得△BFG∽△CGH，
设GH=EF=a，

∴，

∴，

∴BF=，

∴AF=AB-BF=a-，

∴CH=AF= a-，

在Rt△CGH中，
∵CG2+CH2=GH2，
∴42+（a-）2=a2，解得a=或（舍），

∴GH=，

∴BF==，

在Rt△BFG中，

BG=，
∴tan∠BFG==，故③错误；
矩形EFGH的面积=FG×GH=3×=，故④正确．
故选C.