题目内容
如图,AB是⊙O直径,M是⊙O上一点,MN⊥AB,垂足为N、P、Q分别是 弧AM,BM上一点(不与端点重合),如果∠MNP=∠MNQ,
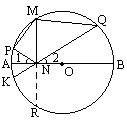
①∠1=∠2;②∠P+∠Q=![]() ;③∠Q=∠PMN;④PM=Om;⑤MN2=PN·QN,其中正确的是
;③∠Q=∠PMN;④PM=Om;⑤MN2=PN·QN,其中正确的是
[ ]
A.①②③
B.①③⑤
C.④⑤
D.①②⑤
答案:B
解析:
提示:
解析:
|
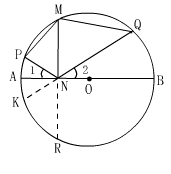
如图:延长QN交⊙O于K,延长MN交⊙O于R,∵MN⊥AB,而∠MNP=∠MNQ,∴∠1=∠2,①正确.∠Q所对的弧为 |
提示:
|
名师导引:延长 QN交⊙O于K,延长MN交⊙O于R,∵MN⊥AB,而∠MNP=∠MNQ,∴∠1=∠2,①正确.∠Q所对的弧为 |

练习册系列答案
 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
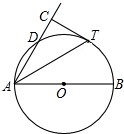 如图,AB是⊙O直径,D为⊙O上一点,AT平分∠BAD交⊙O于点T,过T作AD的垂线交AD的延长线于点C.
如图,AB是⊙O直径,D为⊙O上一点,AT平分∠BAD交⊙O于点T,过T作AD的垂线交AD的延长线于点C.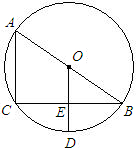 如图,AB是⊙O直径,BC是弦,OD⊥BC于E交弧BC于D.根据中考改编
如图,AB是⊙O直径,BC是弦,OD⊥BC于E交弧BC于D.根据中考改编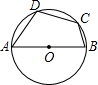 如图,AB是⊙O直径,C、D是⊙O上的两点,若∠BAC=20°,
如图,AB是⊙O直径,C、D是⊙O上的两点,若∠BAC=20°,
 如图,AB是⊙O直径,OB=6,弦CD=10,则弦心距OP的长为( )
如图,AB是⊙O直径,OB=6,弦CD=10,则弦心距OP的长为( ) 如图,AB是⊙O直径,弦CD交AB于E,∠AEC=45°,AB=2.设AE=x,CE2+DE2=y.下列图象中,能表示y与x的函数关系是的( )
如图,AB是⊙O直径,弦CD交AB于E,∠AEC=45°,AB=2.设AE=x,CE2+DE2=y.下列图象中,能表示y与x的函数关系是的( )