��Ŀ����
����Ŀ����ͼ��������y=ax2+bx+c����A���� ![]() ��0����B��3
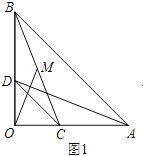
��0����B��3 ![]() ��0����C��0��3�����㣬�߶�BC�������ߵĶԳ����ཻ��D���������ߵĶ���ΪP������PA��AD��DP���߶�AD��y���ཻ�ڵ�E��
��0����C��0��3�����㣬�߶�BC�������ߵĶԳ����ཻ��D���������ߵĶ���ΪP������PA��AD��DP���߶�AD��y���ཻ�ڵ�E�� 
��1����������ߵĽ���ʽ��
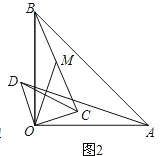
��2����ƽ��ֱ������ϵ���Ƿ���ڵ�Q��ʹ��Q��C��DΪ��������������ADPȫ�ȣ������ڣ������Q�����ꣻ�������ڣ�˵�����ɣ�
��3������CED�Ƶ�E˳ʱ����ת����EC��ת�����߶�BC�ཻ�ڵ�M����ED��ת����Գ����ཻ�ڵ�N������PM��DN����PM=2DN�����N�����ֱ꣨��д���������
���𰸡�
��1��
�⣺�������ߵĽ���ʽΪ��y=a��x+ ![]() ����x��3
����x��3 ![]() ���������C��0��3���ã�
���������C��0��3���ã�
a��0+ ![]() ����0��3
����0��3 ![]() ��=3����� a=��
��=3����� a=�� ![]()
�������ߵĽ���ʽ��y=�� ![]() ��x+
��x+ ![]() ����x��3
����x��3 ![]() ��=��
��=�� ![]() x2+
x2+ ![]() x+3
x+3
��2��
�⣺��ֱ��BC�Ľ���ʽ��y=kx+b�������⣬�У�
![]() ��
��
��� 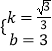 ��
��
��ֱ��BC��y=�� ![]() x+3��
x+3��
�������ߵĽ���ʽ֪��P�� ![]() ��4��������P�ĺ��������ֱ��BC�У��ã�D��
��4��������P�ĺ��������ֱ��BC�У��ã�D�� ![]() ��2����
��2����
���Q��x��y��������
QC2=��x��0��2+��y��3��2=x2+y2��6y+9��QD2=��x�� ![]() ��2+��y��2��2=x2+y2��2
��2+��y��2��2=x2+y2��2 ![]() x��4y+7��
x��4y+7��
����PA2=���� ![]() ��
�� ![]() ��2+��0��4��2=28��AD2=����
��2+��0��4��2=28��AD2=���� ![]() ��
�� ![]() ��2+��0��2��2=16��CD=PD=2��
��2+��0��2��2=16��CD=PD=2��
��QCD�͡�APD�У�CD=PD��������������ȫ�ȣ���
��QC=AP��QD=ADʱ�� ![]()
��QC=AD��QD=APʱ�� ![]()
��١��ڵķ����飬�ã� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
��
���Q��������3 ![]() ��4������
��4������ ![]() ����2��������2
����2��������2 ![]() ��1����0��7��
��1����0��7��
��3��
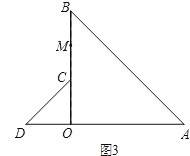
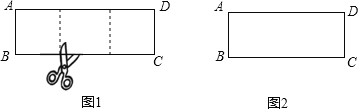
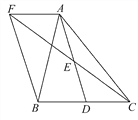
�⣺����������ͼ����ͼ��

��D�� ![]() ��2����B��3
��2����B��3 ![]() ��0��֪��DF=2��BF=2
��0��֪��DF=2��BF=2 ![]() ��
��
���BDF=��ADF=��CDE=��DCE=60�㣬����CED�ǵȱ������Σ�
�ڡ�CEM�͡�DEN�У� 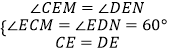
���CEM�ա�DEN���� CM=DN��PM=2CM=2DN��
���M��x���� ![]() x+3��������
x+3��������
PM2=�� ![]() ��x��2+��4+
��x��2+��4+ ![]() x��3��2=
x��3��2= ![]() x2��
x2�� ![]()
![]() x+4��CM2=x2+
x+4��CM2=x2+ ![]() x2=
x2= ![]() x2��
x2��
��֪��PM2=4CM2�����У�
![]() x2��
x2�� ![]()
![]() x+4=4��
x+4=4�� ![]() x2����� x=
x2����� x= ![]() ��
��
��CM=DN= ![]() ��x=
��x= ![]() ��
�� ![]() =
= ![]() ��
��
��FN=DF��DN=2�� ![]() =
= ![]() ��
��
���N�� ![]() ��
�� ![]() ����
����
����������1����֪�����߾������������ֱ꣬�����ô���ϵ������⼴�ɣ���2�����ڵ�Q��λ�ÿ������Ĵ����������ü��η�����Ϊ���ӣ����Կɿ���ֱ����SSS�ж���������ȫ�ȵķ�������⣮��ô������Ҫ֤��CD=DP�������Q�������ʾ��QC��QD�ij���Ȼ�����������Ӧ������з�����ȷ����Q�����꣮��3������B��D�����꣬�����жϳ���CDE�ǵȱ������Σ�Ȼ��ͨ��֤��CEM����DENȫ�����ó�CM=DN�����������M�����꣬��ʾ��PM��CM�ij�����PM=2DN=2CM�з���ȷ����M�����꣬��һ���õ�CM�ij����ɵó�DN�ij����ɴ���õ�N�����꣮

 ����ȫ���ִʾ��ƪ��ϵ�д�
����ȫ���ִʾ��ƪ��ϵ�д� �����߿����ϵ�д�
�����߿����ϵ�д� �㾦�½̲�ȫ�ܽ��ϵ�д�
�㾦�½̲�ȫ�ܽ��ϵ�д�