Question

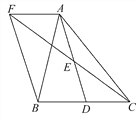
【题目】如图,在△ABC中，D是BC边上的一点,E是AD的中点,过A点作BC的平行线交CE的延长线于点F，且AF=BD,连接BF．

(1)求证：BD=CD；

(2)当△ABC满足什么条件时,四边形AFBD是矩形?并说明理由．

Answer 1

【答案】（1）证明见解析（2）当△ABC满足:AB=AC时,四边形AFBD是矩形.

【解析】分析：（1）由AF与BC平行，利用两直线平行内错角相等得到一对角相等，再一对对顶角相等，且由E为AD的中点，得到AE=DE，利用AAS得到△AFE与△DCE全等，利用全等三角形的对应边相等即可得证；

（2）当△ABC满足：AB=AC时，四边形AFBD是矩形，理由为：由AF与BD平行且相等，得到四边形AFBD为平行四边形，再由AB=AC，BD=CD，利用三线合一得到AD垂直于BC，即∠ADB为直角，即可得证．

详解：(1)∵AF∥BC，

∴∠AFE=∠DCE.

∵E是AD的中点，

∴AE=DE .

在△AEF和△DEC中，

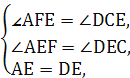
∴△AEF≌△DEC(AAS)，

∴AF=CD.

∵AF=BD，

∴BD=CD.

(2)当△ABC满足:AB=AC时,四边形AFBD是矩形.

理由如下:

∵AF∥BD,AF=BD,

∴四边形AFBD是平行四边形,

∵AB=AC,BD=CD,

∴∠ADB=90°,

∴平行四边形AFBD是矩形.