题目内容
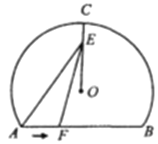
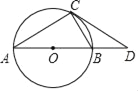
【题目】如图,AB是⊙O的直径,CD与⊙O相切于点C,与AB的延长线交于D.
(1)求证:△ADC∽△CDB;
(2)若AC=2,AB=![]() CD,求⊙O半径.
CD,求⊙O半径.
【答案】(1)见解析;(2)![]()
【解析】分析: (1)首先连接CO,根据CD与⊙O相切于点C,可得:∠OCD=90°;然后根据AB是圆O的直径,可得:∠ACB=90°,据此判断出∠CAD=∠BCD,即可推得△ADC∽△CDB.
(2)首先设CD为x,则AB=32x,OC=OB=34x,用x表示出OD、BD;然后根据△ADC∽△CDB,可得:ACCB=CDBD,据此求出CB的值是多少,即可求出⊙O半径是多少.
详解:
(1)证明:如图,连接CO,
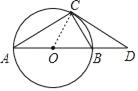 ,
,
∵CD与⊙O相切于点C,
∴∠OCD=90°,
∵AB是圆O的直径,
∴∠ACB=90°,
∴∠ACO=∠BCD,
∵∠ACO=∠CAD,
∴∠CAD=∠BCD,
在△ADC和△CDB中,
![]()
∴△ADC∽△CDB.
(2)解:设CD为x,
则AB=![]() x,OC=OB=
x,OC=OB=![]() x,
x,
∵∠OCD=90°,
∴OD=![]() =
=![]() =
=![]() x,
x,
∴BD=OD﹣OB=![]() x﹣
x﹣![]() x=
x=![]() x,
x,
由(1)知,△ADC∽△CDB,
∴![]() =
=![]() ,
,
即![]() ,
,
解得CB=1,
∴AB=![]() =
=![]() ,
,
∴⊙O半径是![]() .
.
点睛: 此题主要考查了切线的性质和应用,以及勾股定理的应用,要熟练掌握.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目