题目内容
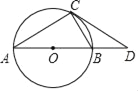
【题目】如图，点C是⊙O优弧ACB上的中点，弦AB=6cm，E为OC上任意一点，动点F从点A出发，以每秒1cm的速度沿AB方向响点B匀速运动，若y=AE－EF,则y与动点F的运动时间x（0≤x≤6 ）秒的函数关系式为 .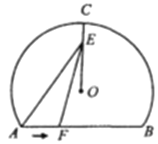
【答案】y=x2－6x
【解析】
首先延长CO交AB于G，根据垂径定理的知识，可得CO⊥AB，并可求得AG的值，由勾股定理可得AE2=AG2+EG2，EF2=FG2+EG2，即可求得y=AG2-FG2，即可求得函数关系式．
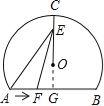
解：延长CO交AB于G，
∵点C是⊙O优弧ACB上的中点，
∴CO⊥AB，AG=
AB=×6=3（cm），
∴AE2=AG2+EG2，EF2=FG2+EG2，
当0≤x≤3时，AF=xcm，FG=（3-x）cm，
∴y=AE2-EF2=AG2+EG2-FG2-EG2=AG2-FG2=9-（3-x）2=6x-x2；
当3＜x≤6时，AF=xcm，FG=（x-3）cm，
∴y=AE2-EF2=AG2+EG2-FG2-EG2=AG2-FG2=9-（x-3）2=6x-x2．
故答案为：y=6x-x2．
练习册系列答案
名校练考卷期末冲刺卷系列答案
相关题目
【题目】王勇和李明两位同学在学习“概率”时，做投掷骰子（质地均匀的正方体）实验，他们共做了30次实验，实验的结果如下：
朝上的点数 | 1 | 2 | 3 | 4 | 5 | 6 |
出现的次数 | 2 | 5 | 6 | 4 | 10 | 3 |
（1）分别计算这30次实验中“3点朝上”的频率和“5点朝上”的频率；
（2）王勇说：“根据以上实验可以得出结论：由于5点朝上的频率最大，所以一次实验中出现5点朝上的概率最大”；李明说：“如果投掷300次，那么出现6点朝上的次数正好是30次”．试分别说明王勇和李明的说法正确吗？并简述理由；
（3）现王勇和李明各投掷一枚骰子，请用列表或画树状图的方法求出两枚骰子朝上的点数之和为3的倍数的概率．
