题目内容
【题目】任意抛掷一枚骰子两次，骰子停止转动后，计算朝上的点数的和．
（1）和最小的是多少，和最大的是多少？
（2）下列事件：①点数的和为7；②点数的和为1；③点数的和为15．哪些是不可能性事件？哪些是不确定事件？
（3）点数的和为7与点数的和为2的可能性谁大？请说明理由．
【答案】⑴ 和最小是２；和最大是12
⑵不可能事件是②③；不确定事件是①．
（3）P(和为7)=
；P(和为2)=
；和为7的可能性要大．
【解析】
（1）可用用列表法或画树状图法可得到所有情况，从而得到和最小的值，和最大的值；
（2）根据所有的情况可得不可能事件是②③；不确定事件是①；
可用用列表法或画树状图法可得到所有情况，从而得到点数的和为7与点数的和为2的概率，比较后可得可能性谁大。
桃李文化快乐暑假武汉出版社系列答案
优秀生快乐假期每一天全新寒假作业本系列答案
暑假接力赛新疆青少年出版社系列答案【题目】王勇和李明两位同学在学习“概率”时，做投掷骰子（质地均匀的正方体）实验，他们共做了30次实验，实验的结果如下：
朝上的点数 | 1 | 2 | 3 | 4 | 5 | 6 |
出现的次数 | 2 | 5 | 6 | 4 | 10 | 3 |
（1）分别计算这30次实验中“3点朝上”的频率和“5点朝上”的频率；
（2）王勇说：“根据以上实验可以得出结论：由于5点朝上的频率最大，所以一次实验中出现5点朝上的概率最大”；李明说：“如果投掷300次，那么出现6点朝上的次数正好是30次”．试分别说明王勇和李明的说法正确吗？并简述理由；
（3）现王勇和李明各投掷一枚骰子，请用列表或画树状图的方法求出两枚骰子朝上的点数之和为3的倍数的概率．
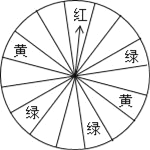
【题目】“六一”儿童节期间，某商厦为了吸引顾客，设立了一个可以自由转动的转盘（转盘被平均分成16份），并规定：顾客每购买100元的商品，就能获得一次转动转盘的机会．如果转盘停止后，指针正好对准哪个区域，顾客就可以获得相应的奖品．
颜色 | 奖品 |
红色 | 玩具熊 |
黄色 | 童话书 |
绿色 | 彩笔 |
小明和妈妈购买了125元的商品，请你分析计算：
(1)小明获得奖品的概率是多少？
(2)小明获得童话书的概率是多少？
