题目内容
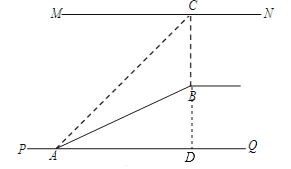
【题目】(本小题满分8分) 如图1,某超市从底楼到二楼有一自动扶梯,图2是侧面示意图.已知自动扶梯AB的坡度为1:2.4,AB的长度是13米,MN是二楼楼顶,MN∥PQ,C是MN上处在自动扶梯顶端B点正上方的一点,BC⊥MN,在自动扶梯底端A处测得C点的仰角为42°,求二楼的层高BC(精确到0.1米).(参考数据:sin42°≈0.67,cos42°≈0.74,tan42°≈0.90)
【答案】约为5.8米.
【解析】试题分析:延长CB交PQ于点D,根据坡度的定义即可求得BD的长,然后在直角△CDA中利用三角函数即可求得CD的长,则BC即可得到.
试题解析:延长CB交PQ于点D.
∵MN∥PQ,BC⊥MN,
∴BC⊥PQ.
∵自动扶梯AB的坡度为1:2.4,
∴![]() .
.
设BD=5k米,AD=12k米,则AB=13k米.
∵AB=13米,
∴k=1,
∴BD=5米,AD=12米.
在Rt△CDA中,∠CDA=90゜,∠CAD=42°,
∴CD=ADtan∠CAD≈12×0.90≈10.8米,
∴BC≈5.8米.
答:二楼的层高BC约为5.8米.

练习册系列答案
相关题目
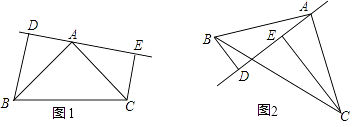
【题目】如图,已知AB=AC,AE=AF,BE与CF交于点D,则对于下列结论:①△ABE≌△ACF;②△BDF≌△CDE;③D在∠BAC的平分线上.其中正确的是( ) 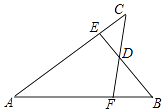
A.①
B.②
C.①和②
D.①②③