题目内容
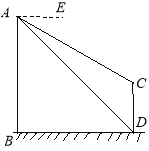
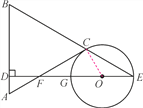
【题目】如图,△ABC中,AB=AC,点E是线段BC延长线上一点,ED⊥AB,垂足为D,ED交线段AC于点F,点O在线段EF上,⊙O经过C、E两点,交ED于点G.
(1)求证:AC是⊙O的切线;
(2)若∠E=30°,AD=1,BD=5,求⊙O的半径.
【答案】(1)证明见解析(2)![]()
【解析】
(1)证明:连接CO.
∵AB=AC,
∴∠B=∠ACB.
∵OC=OE,
∴∠OCE=∠E.
∵ED⊥AB,
∴∠BDE=90°.
∴∠B+∠E=90°.∴∠ACB+∠OCE=90°.
∴∠ACO=90°,即AC⊥OC.
∴AC是⊙O的切线.
(2)∵∠E=30°,∴∠OCE=30°.∴∠FCE=120°.
∴∠CFO=30°.∴∠AFD=∠CFO=30°.
∵AD=1,∴DF=![]() .
.
∵BD=5,∴DE=![]() .∴EF=
.∴EF=![]() .
.
∵OF=2OC,∴EF=3OE=![]() .
.
∴OE=![]() ,即⊙O的半径为
,即⊙O的半径为![]() .
.

练习册系列答案
相关题目