题目内容
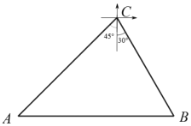
【题目】如图,将一块直角三角形纸板的直角顶点放在C(1,![]() )处,两直角边分别与x,y轴平行,纸板的另两个顶点A,B恰好是直线y=kx+
)处,两直角边分别与x,y轴平行,纸板的另两个顶点A,B恰好是直线y=kx+![]() 与双曲线y=
与双曲线y=![]() (m>0)的交点.
(m>0)的交点.
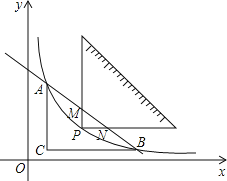
(1)求m和k的值;
(2)设双曲线y=![]() (m>0)在A,B之间的部分为L,让一把三角尺的直角顶点P在L上滑动,两直角边始终与坐标轴平行,且与线段AB交于M,N两点,请探究是否存在点P使得MN=
(m>0)在A,B之间的部分为L,让一把三角尺的直角顶点P在L上滑动,两直角边始终与坐标轴平行,且与线段AB交于M,N两点,请探究是否存在点P使得MN=![]() AB,写出你的探究过程和结论.
AB,写出你的探究过程和结论.
【答案】(1)k=﹣![]() ;m=4 ;(2)不存在,理由见解析.
;m=4 ;(2)不存在,理由见解析.
【解析】
(1)由题意易知点A横坐标为1,代入y=![]() ,可用含m的代数式表示它的纵坐标;同理可表示点B坐标,再代入方程组
,可用含m的代数式表示它的纵坐标;同理可表示点B坐标,再代入方程组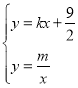 即可求m和k的值;
即可求m和k的值;
(2)用反证法证明.假设存在,运用一元二次方程判别式即可解出.
解:(1)∵A,B在双曲线y=![]() (m>0)上,AC∥y轴,BC∥x轴,
(m>0)上,AC∥y轴,BC∥x轴,
∴A,B的坐标分别(1,m),(2m,![]() )
)
又点A,B在直线y=kx+![]() 上,
上,
∴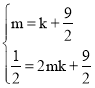
解得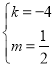 或
或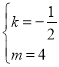
当k=﹣4且m=![]() 时,点A,B的坐标都是(1,
时,点A,B的坐标都是(1,![]() ),不合题意,应舍去;
),不合题意,应舍去;
当k=﹣![]() 且m=4时,点A,B的坐标分别为(1,4),(8,
且m=4时,点A,B的坐标分别为(1,4),(8,![]() ,符合题意.
,符合题意.
∴k=﹣![]() ,m=4.
,m=4.
(2)假设存在点P使得MN=![]() AB.
AB.
∵AC∥y轴,MP∥y轴,
∴AC∥MP,
∴∠PMN=∠CAB,
∴Rt△ACB∽Rt△MPN,
∴![]() ,
,
设点P坐标为P(x,![]() )(1<x<8),
)(1<x<8),
∴M点坐标为M(x,﹣![]() x+
x+![]() ),
),
∴MP=﹣![]() x+
x+![]() -
-![]() .
.
又∵AC=4﹣![]() ,
,
∴![]() ,即2x2﹣11x+16=0(※)
,即2x2﹣11x+16=0(※)
∵△=(﹣11)2﹣4×2×16=﹣7<0.
∴方程(※)无实数根.
∴不存在点P使得MN=![]() AB.
AB.

【题目】一次安全知识测验中,学生得分均为整数,满分10分,成绩达到9分为优秀,这次测验中甲、乙两组学生人数相同,成绩如下统计图:

(1)在乙组学生成绩统计图中,8分所在的扇形的圆心角为___________度
(2)请补充完整下面的成绩统计分析表:
平均数 | 方差 | 众数 | 中位数 | 优秀率 | |
甲组 | 7 | 1.8 | 7 | 7 |
|
乙组 | 1.36 |
|
(3)你认为那组成绩较好?从以上信息中写出两条支持你的选择
(4)从甲、乙两组得9分的学生中抽取两人参加市级比赛,求这两人来自不同组的概率