题目内容
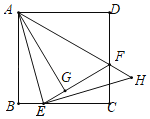
【题目】如图,已知正方形ABCD的边长为3,E是边BC上一点,BE=1,将△ABE,△ADF分别沿折痕AE,AF向内折叠,点B,D在点G处重合,过点E作EH⊥AE,交AF的延长线于H,则线段FH的长为_______.
【答案】![]()
【解析】
设DF=FG=x,在Rt△EFC中,由EF=1+x,EC=3﹣1=2,FC=3﹣x,根据勾股定理构建方程求出x,再求出AF,AH即可解决问题.
解:∵四边形ABCD是正方形,
∴∠B=∠C=∠D=∠BAD=90°,AB=BC=CD=AD=3,
设DF=FG=x,
在Rt△EFC中,∵EF=1+x,EC=3﹣1=2,FC=3﹣x,
∴(x+1)2=22+(3﹣x)2,
解得x=![]()
∴AF=![]() =
= =
=![]() ,AE=
,AE=![]() =
=![]() =
=![]() ,
,
由翻折的性质可知,∠DAF=∠GAF,∠EAB=∠EAG,
∴∠EAH=45°,
∵EH⊥EA,
∴∠AEH=90°,
∴AE=EH=![]() ,AH=
,AH=![]() AE=2
AE=2![]() ,
,
∴FH=AH﹣AF=2![]() ﹣
﹣![]() =
=![]() ,
,
故答案为:![]() .
.

练习册系列答案
相关题目
【题目】一次安全知识测验中,学生得分均为整数,满分10分,成绩达到9分为优秀,这次测验中甲、乙两组学生人数相同,成绩如下统计图:

(1)在乙组学生成绩统计图中,8分所在的扇形的圆心角为___________度
(2)请补充完整下面的成绩统计分析表:
平均数 | 方差 | 众数 | 中位数 | 优秀率 | |
甲组 | 7 | 1.8 | 7 | 7 |
|
乙组 | 1.36 |
|
(3)你认为那组成绩较好?从以上信息中写出两条支持你的选择
(4)从甲、乙两组得9分的学生中抽取两人参加市级比赛,求这两人来自不同组的概率





