Question

【题目】如图，P是抛物线y=x2﹣4x+3上的一点，以点P为圆心、1个单位长度为半径作⊙P，当⊙P与直线y=0相切时，点P的坐标为 ．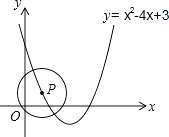

Answer 1

【答案】（2+ ，1）或（2﹣ ，1）或（2，﹣1）
【解析】解：当y=1时，x2﹣4x+3=1， 解得：x=2± ，
∴P（2+ ，1）或（2﹣ ，1），
当y=﹣1时，x2﹣4x+3=﹣1，
解得：x1=x2=2，
∴P（2，﹣1），
则点P的坐标为：（2+ ，1）或（2﹣ ，1）或（2，﹣1）．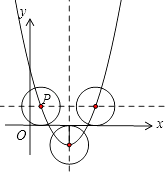

⊙P与直线y=0相切时就是：⊙P与x轴相切，半径为1个单位长度，即点P的纵坐标|y|=1，根据P是抛物线y=x2﹣4x+3上的一点，代入计算出x的值，并写出点P的坐标，一共有3种可能．