题目内容
在等腰Rt△ABC中,∠C=90°,AC=1,过点C作直线 ∥AB,F是
∥AB,F是 上的一点,且AB=AF,则点F到直线BC的距离为__________
上的一点,且AB=AF,则点F到直线BC的距离为__________
 ∥AB,F是
∥AB,F是 上的一点,且AB=AF,则点F到直线BC的距离为__________
上的一点,且AB=AF,则点F到直线BC的距离为__________
分析:如图,延长AC,做FD⊥BC交点为D,FE⊥AC,交点为E,可得四边形CDFE是正方形,则,CD=DF=FE=EC;等腰Rt△ABC中,∠C=90°,AC=1,所以,可求出AC=1,AB=  ,又AB=AF;所以,在直角△AEF中,可运用勾股定理求得DF的长即为点F到BC的距离.
,又AB=AF;所以,在直角△AEF中,可运用勾股定理求得DF的长即为点F到BC的距离.
解答:解:(1)如图,延长AC,做FD⊥BC交点为D,FE⊥AC,交点为E,
∵CF∥AB,∴∠FCD=∠CBA=45°,

∴四边形CDFE是正方形,
即,CD=DF=FE=EC,
∵在等腰直角△ABC中,AC=BC=1,AB=AF,
∴AB= =
= ,
,
∴AF= ;
;
∴在直角△AEF中,(1+EC)2+EF2=AF2
∴(1+DF)2+DF2=( )2,
)2,
解得,DF= ;
;
(2)如图,延长BC,做FD⊥BC,交点为D,延长CA,做FE⊥CA于点E,
同理可证,四边形CDFE是正方形,
即,CD=DF=FE=EC,
同理可得,在直角△AEF中,(EC-1)2+EF2=AF2,
∴(FD-1)2+FD2=( )2,
)2,
解得,FD= 故答案为:
故答案为: .
.
 ,又AB=AF;所以,在直角△AEF中,可运用勾股定理求得DF的长即为点F到BC的距离.
,又AB=AF;所以,在直角△AEF中,可运用勾股定理求得DF的长即为点F到BC的距离.解答:解:(1)如图,延长AC,做FD⊥BC交点为D,FE⊥AC,交点为E,
∵CF∥AB,∴∠FCD=∠CBA=45°,

∴四边形CDFE是正方形,
即,CD=DF=FE=EC,
∵在等腰直角△ABC中,AC=BC=1,AB=AF,
∴AB=
 =
= ,
,∴AF=
 ;
;∴在直角△AEF中,(1+EC)2+EF2=AF2
∴(1+DF)2+DF2=(
 )2,
)2,解得,DF=
 ;
;(2)如图,延长BC,做FD⊥BC,交点为D,延长CA,做FE⊥CA于点E,

同理可证,四边形CDFE是正方形,
即,CD=DF=FE=EC,
同理可得,在直角△AEF中,(EC-1)2+EF2=AF2,
∴(FD-1)2+FD2=(
 )2,
)2,解得,FD=
 故答案为:
故答案为: .
.
练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
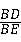 =
=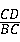 ;
;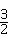 AB,求tan∠CDF的值.
AB,求tan∠CDF的值.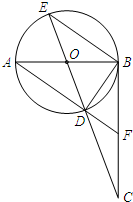

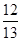

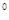 和 10
和 10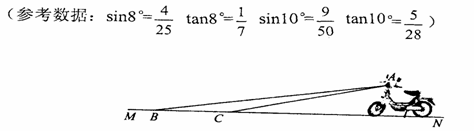

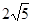 ,则BE的长为
,则BE的长为 


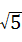 ,BC=2,则sin∠ACD的值为( )
,BC=2,则sin∠ACD的值为( )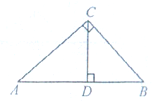
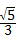 B、
B、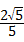
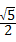 D、
D、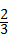

 ,AE=
,AE= ,
,