题目内容
如图,一次函数y=2x﹣2的图象与x轴、y轴分别相交于B、A两点,与反比例函数 的图象在第一象限内的交点为M(3,m).
的图象在第一象限内的交点为M(3,m).
(1)求反比例函数的解析式;
(2)在x轴上是否存在点P,使AM⊥PM?若存在,求出点P的坐标;若不存在,说明理由.
(1)y=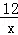 (2)存在.理由见解析
(2)存在.理由见解析
解析试题分析:(1)先把M(3,m)代入y=2x﹣2求出m,确定M点的坐标,然后利用待定系数法确定反比例函数解析式;
(2)先确定A点坐标为(0,﹣2),B点坐标为(1,0),再根据勾股定理计算出AB= ;根据M点坐标得到MC=4,BC=2,则利用勾股定理可计算出BM=2
;根据M点坐标得到MC=4,BC=2,则利用勾股定理可计算出BM=2 ,然后证明Rt△OBA∽Rt△MBP,利用相似比计算出BP,于是可确定P点坐标.
,然后证明Rt△OBA∽Rt△MBP,利用相似比计算出BP,于是可确定P点坐标.
解:(1)把M(3,m)代入y=2x﹣2得m=2×3﹣2=4,
∴M点坐标为(3,4),
把M(3,4)代入y=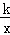 得k=3×4=12,
得k=3×4=12,
∴反比例函数的解析式为y=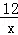 ;
;
(2)存在.
作MC⊥x轴于C,如图,
把x=0代入y=2x﹣2得y=﹣2;把y=0代入y=2x﹣2得2x﹣2=0,解得x=1,
∴A点坐标为(0,﹣2),B点坐标为(1,0),
∴OA=2,OB=1,
在Rt△OAB中,AB= =
=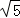 ,
,
∵M点坐标为(3,4),
∴MC=4,BC=3﹣1=2,
在Rt△MBC中,MB=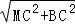 =2
=2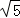 ,
,
∵MA⊥MB,
∴∠BMP=90°,
而∠OBA=∠MBP,
∴Rt△OBA∽Rt△MBP,
∴ =
=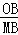 ,即
,即 =
= ,
,
∴BP=10,
∴OP=11,
∴点P的坐标为(11,0).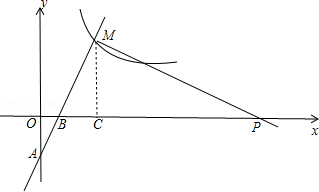
点评:本题考查了反比例函数的综合题:掌握反比例函数图象上点的坐标特征和待定系数法确定函数解析式;熟练运用勾股定理和相似比进行几何计算.

练习册系列答案
相关题目
 (m为常数)图象的一支.
(m为常数)图象的一支.
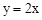 图象在第一象限的交点为A(2,n),求点A的坐标及反比例函数的解析式.
图象在第一象限的交点为A(2,n),求点A的坐标及反比例函数的解析式. 与反比例函数
与反比例函数 的图象交于A、B两点,与x轴交于点C,已知点A的坐标为(-1,m).
的图象交于A、B两点,与x轴交于点C,已知点A的坐标为(-1,m).
 与边BC交于点D(4,m),与边AB交于点E(2,n).
与边BC交于点D(4,m),与边AB交于点E(2,n).
 ,求k的值和点B的坐标.
,求k的值和点B的坐标.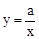 (a≠0,x>0)分别交于D、E两点.
(a≠0,x>0)分别交于D、E两点.
 (x>0)的图象经过点B,过点B作BC⊥x轴于点C,点P是该反比例函数图象上任意一点,过点P作PD⊥x轴于点D,点Q是线段AB上任意一点,连接OQ、CQ.
(x>0)的图象经过点B,过点B作BC⊥x轴于点C,点P是该反比例函数图象上任意一点,过点P作PD⊥x轴于点D,点Q是线段AB上任意一点,连接OQ、CQ.
 (x>0,k≠0)的图像经过线段BC的中点D.
(x>0,k≠0)的图像经过线段BC的中点D.

