题目内容
在平面直角坐标系中,点A(﹣3,4)关于y轴的对称点为点B,连接AB,反比例函数 (x>0)的图象经过点B,过点B作BC⊥x轴于点C,点P是该反比例函数图象上任意一点,过点P作PD⊥x轴于点D,点Q是线段AB上任意一点,连接OQ、CQ.
(x>0)的图象经过点B,过点B作BC⊥x轴于点C,点P是该反比例函数图象上任意一点,过点P作PD⊥x轴于点D,点Q是线段AB上任意一点,连接OQ、CQ.
(1)求k的值;
(2)判断△QOC与△POD的面积是否相等,并说明理由.
(1)k=12。
(2)相等。理由见解析
解析试题分析:(1)根据点B与点A关于y轴对称,求出B点坐标,再代入反比例函数解析式解可求出k的值;
(2)设点P的坐标为(m,n),点P在反比例函数 (x>0)的图象上,求出S△POD,根据AB∥x轴,OC=3,BC=4,点Q在线段AB上,求出S△QOC,二者比较即可。
(x>0)的图象上,求出S△POD,根据AB∥x轴,OC=3,BC=4,点Q在线段AB上,求出S△QOC,二者比较即可。
解:(1)∵点B与点A关于y轴对称,A(﹣3,4),
∴点B的坐标为(3,4)。
∵反比例函数 (x>0)的图象经过点B,
(x>0)的图象经过点B,
∴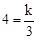 ,解得k=12。
,解得k=12。
(2)相等。理由如下:
设点P的坐标为(m,n),其中m>0,n>0,
∵点P在反比例函数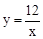 (x>0)的图象上,
(x>0)的图象上,
∴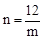 ,即mn=12。∴S△POD=
,即mn=12。∴S△POD=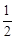 OD•PD=
OD•PD=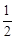 mn=
mn=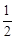 ×12=6。
×12=6。
∵A(﹣3,4),B(3,4),∴AB∥x轴,OC=3,BC=4。
∵点Q在线段AB上,∴S△QOC=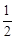 OC•BC=
OC•BC=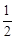 ×3×4=6。
×3×4=6。
∴S△QOC=S△POD。

练习册系列答案
相关题目
如图,属于同位角是( )
| A.∠1和∠2 | B.∠1和∠3 |
| C.∠1和∠4 | D.∠2和∠3 |
 的图象与一次函数y=kx+b的图象相交于两点A(m,3)和B(﹣3,n).
的图象与一次函数y=kx+b的图象相交于两点A(m,3)和B(﹣3,n).
 (x>
(x> )图象上一点P,PA⊥x轴于点A(a,0),点B坐标为(0,b)(b>0),动点M是y轴正半轴上B点上方的点,动点N在射线AP上,过点B作AB的垂线,交射线AP于点D,交直线MN于点Q,连结AQ,取AQ的中点为C.
)图象上一点P,PA⊥x轴于点A(a,0),点B坐标为(0,b)(b>0),动点M是y轴正半轴上B点上方的点,动点N在射线AP上,过点B作AB的垂线,交射线AP于点D,交直线MN于点Q,连结AQ,取AQ的中点为C.
 ,求此时P点的坐标;
,求此时P点的坐标; (k≠0)和一次函数y=x﹣6.
(k≠0)和一次函数y=x﹣6. 的图象在第一象限内的交点为M(3,m).
的图象在第一象限内的交点为M(3,m).
 (x≠﹣1)的图象在第一象限内的交点为P(x0,3).
(x≠﹣1)的图象在第一象限内的交点为P(x0,3).
