题目内容
(2013年四川资阳9分)如图,已知直线l分别与x轴、y轴交于A,B两点,与双曲线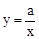 (a≠0,x>0)分别交于D、E两点.
(a≠0,x>0)分别交于D、E两点.
(1)若点D的坐标为(4,1),点E的坐标为(1,4):
①分别求出直线l与双曲线的解析式;
②若将直线l向下平移m(m>0)个单位,当m为何值时,直线l与双曲线有且只有一个交点?
(2)假设点A的坐标为(a,0),点B的坐标为(0,b),点D为线段AB的n等分点,请直接写出b的值.
解:(1)①把D(4,1)代入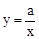 得a=1×4=4,
得a=1×4=4,
∴反比例函数解析式为 (x>0)。
(x>0)。
设直线l的解析式为y=kx+t,
把D(4,1),E(1,4)代入得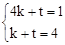 ,解得
,解得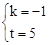 。
。
∴直线l的解析式为y=﹣x+5。
②直线l向下平移m(m>0)个单位得到y=﹣x+5﹣m,
当方程组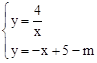 只有一组解时,直线l与双曲线有且只有一个交点,
只有一组解时,直线l与双曲线有且只有一个交点,
化为关于x的方程得x2+(5﹣m)x+4=0,
△=(m﹣5)2﹣4×4=0,解得m1=1,m2=9。
而m=9时,解得x=﹣2,故舍去。
∴当m=1时,直线l与双曲线有且只有一个交点。
(2)如图,作DF⊥x轴于点F,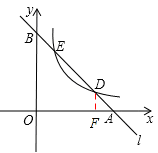
∵点D为线段AB的n等分点,∴DA:AB=1:n。
∵DF∥OB,∴△ADF∽△ABO。
∴ ,即
,即 。
。
∴ 。∴OF=
。∴OF= 。
。
∴D点坐标为( ,
, )。
)。
把D( ,
, )代入
)代入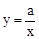 得(
得( )•
)• =a,解得
=a,解得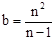 。
。
解析

练习册系列答案
相关题目
如图,下列推理错误的是( )
| A.∵∠1=∠2,∴c∥d | B.∵∠3=∠4,∴c∥d |
| C.∵∠1=∠3,∴ a∥b | D.∵∠1=∠4,∴a∥b |
 .
. 是反比例函数
是反比例函数 (k>0)在第一象限图象上的两点,点
(k>0)在第一象限图象上的两点,点 的坐标为(2,0),若△
的坐标为(2,0),若△ 与△
与△ 均为等边三角形.
均为等边三角形.
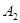 点的坐标.
点的坐标. 交于点B(2,1).
交于点B(2,1).
 的一部分.请根据图中信息解答下列问题:
的一部分.请根据图中信息解答下列问题:
 的图象经过点C,点P在反比例函数图象上且位于C点左侧,过点P作x轴、y轴的垂线分别交直线l于M、N两点.
的图象经过点C,点P在反比例函数图象上且位于C点左侧,过点P作x轴、y轴的垂线分别交直线l于M、N两点.
 的图象在第一象限内的交点为M(3,m).
的图象在第一象限内的交点为M(3,m).

 爸买了今年七月份去上海看世博会的一张门票,她和哥哥两人都很想去观看,可门票只有一张,读九年级的哥哥想了一个办法,拿了八张扑克牌,
爸买了今年七月份去上海看世博会的一张门票,她和哥哥两人都很想去观看,可门票只有一张,读九年级的哥哥想了一个办法,拿了八张扑克牌, 为偶数,则小莉去;如果和为奇数,则哥哥去.
为偶数,则小莉去;如果和为奇数,则哥哥去.