题目内容
如果△ABC∽△DEF,△ABC的三边长为2、3、4,△DEF的一边长为8,那么△DEF的周长不可能是
- A.18
- B.24
- C.30
- D.36
C
分析:由△ABC的三边长为2、3、4,即可求得△ABC的周长,然后根据相似三角形周长的比等于相似比,分别从8为最长边,最短边或中间边去分析即可求得答案.
解答:∵△ABC的三边长为2、3、4,
∴△ABC的周长为:2+3+4=9,
∵△ABC∽△DEF,△DEF的一边长为8,
若DE=8,则 ,
,
即: ,
,
∴△DEF的周长为36;
若DF=8,则 ,
,
即: ,
,
∴△DEF的周长为18;
若EF=8,则 ,
,
即 ,
,
∴△DEF的周长为24.
故选C.
点评:此题考查了相似三角形的性质.解题的关键是注意掌握相似三角形周长的比等于相似比定理的应用.
分析:由△ABC的三边长为2、3、4,即可求得△ABC的周长,然后根据相似三角形周长的比等于相似比,分别从8为最长边,最短边或中间边去分析即可求得答案.
解答:∵△ABC的三边长为2、3、4,
∴△ABC的周长为:2+3+4=9,
∵△ABC∽△DEF,△DEF的一边长为8,
若DE=8,则
 ,
,即:
 ,
,∴△DEF的周长为36;
若DF=8,则
 ,
,即:
 ,
,∴△DEF的周长为18;
若EF=8,则
 ,
,即
 ,
,∴△DEF的周长为24.
故选C.
点评:此题考查了相似三角形的性质.解题的关键是注意掌握相似三角形周长的比等于相似比定理的应用.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
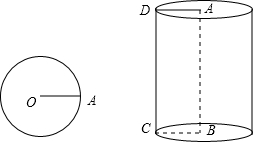 (1)填空:如图,我们知道,一条线段OA绕着它的一个端点O旋转一周,另一个端点所形成的图形叫做
(1)填空:如图,我们知道,一条线段OA绕着它的一个端点O旋转一周,另一个端点所形成的图形叫做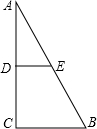
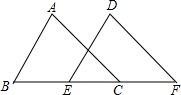 (2013•十堰模拟)如图,在△ABC与△DEF中,如果AB=DE,BE=CF,∠ABC=∠DEF
(2013•十堰模拟)如图,在△ABC与△DEF中,如果AB=DE,BE=CF,∠ABC=∠DEF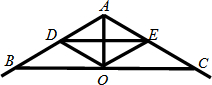 如图,为了加固房屋,要在屋架上加一根横梁DE,使DE∥BC.如果∠ABC=31°,∠ADE应为多少度?
如图,为了加固房屋,要在屋架上加一根横梁DE,使DE∥BC.如果∠ABC=31°,∠ADE应为多少度? 在图中△ABC的外部任取一点P,连接PA、PB、PC,分别取PA、PB、PC的中点D、E、F,连接DE、EF、DF.
在图中△ABC的外部任取一点P,连接PA、PB、PC,分别取PA、PB、PC的中点D、E、F,连接DE、EF、DF.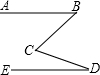 如图:如果AB∥DE,∠ABC=30°,∠CDE=25°,那么∠BCD=
如图:如果AB∥DE,∠ABC=30°,∠CDE=25°,那么∠BCD=