题目内容
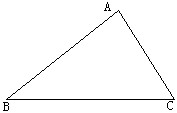
 在图中△ABC的外部任取一点P,连接PA、PB、PC,分别取PA、PB、PC的中点D、E、F,连接DE、EF、DF.
在图中△ABC的外部任取一点P,连接PA、PB、PC,分别取PA、PB、PC的中点D、E、F,连接DE、EF、DF.(1)△ABC与△DEF相似吗?为什么?
(2)如果△ABC的周长为24,求△DEF的周长.
分析:(1)相似,利用三角形的中位线定理,可以得到两个三角形的对应边的比相等,根据三边的比对应相等的三角形相似即可证得;
(2)两个三角形相似,且已知相似比,根据相似三角形的周长的比等于相似比即可求解.
(2)两个三角形相似,且已知相似比,根据相似三角形的周长的比等于相似比即可求解.
解答: 解:(1)相似.
解:(1)相似.
理由:∵D,E是PA,PB的中点,
∴DE=
AB,
∴
=
,
同理,
=
,
=
,
∴
=
=
=
,
∴△ABC∽△DEF;
(2)∵△ABC∽△DEF,且
=
=
=
,
∴△DEF的周长是:
×24=12.
 解:(1)相似.
解:(1)相似.理由:∵D,E是PA,PB的中点,
∴DE=
| 1 |
| 2 |
∴
| DE |
| AB |
| 1 |
| 2 |
同理,
| DF |
| AC |
| 1 |
| 2 |
| EF |
| BC |
| 1 |
| 2 |
∴
| DE |
| AB |
| DF |
| AC |
| EF |
| BC |
| 1 |
| 2 |
∴△ABC∽△DEF;
(2)∵△ABC∽△DEF,且
| DE |
| AB |
| DF |
| AC |
| EF |
| BC |
| 1 |
| 2 |
∴△DEF的周长是:
| 1 |
| 2 |
点评:本题考查了三角形的中位线定理,以及相似三角形的判定与性质,正确证明两个三角形的对应边的比相等是关键.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
 如图,△ABC中,∠A=90°以直角边AB为边,在三角形ABC的外部作正方形ABDE,AF是斜边BC的高,延长FA使AG=BC.
如图,△ABC中,∠A=90°以直角边AB为边,在三角形ABC的外部作正方形ABDE,AF是斜边BC的高,延长FA使AG=BC. 在图中△ABC的外部任取一点P,连接PA、PB、PC,分别取PA、PB、PC的中点D、E、F,连接DE、EF、DF.
在图中△ABC的外部任取一点P,连接PA、PB、PC,分别取PA、PB、PC的中点D、E、F,连接DE、EF、DF.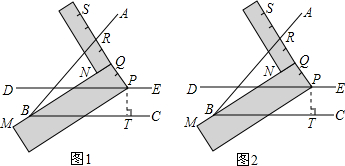 (1)阅读理解:
(1)阅读理解: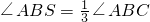 是否成立?如果成立,请说明理由;如果不成立,请在图2中∠ABC的外部画出
是否成立?如果成立,请说明理由;如果不成立,请在图2中∠ABC的外部画出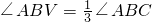 (无需写画法,保留画图痕迹即可).
(无需写画法,保留画图痕迹即可).