题目内容
【题目】一艘货轮以34海里/时的速度在海面上向正南方向航行,当它行驶至B处时,某观察者发现在货轮的北偏东75°方向有一灯塔C;货轮继续向南航行1.5小时后到达A处,某观察者再次发现灯塔C在货轮的东北方向.求此时货轮与灯塔C的距离.(结果保留到个位)(参考数据:sin75°≈0.97,cos75°≈0.29,tan75°≈3.73,![]()
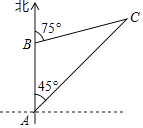
【答案】98海里.
【解析】
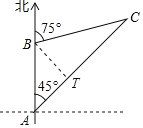
过B作BT⊥AC于T,根据正切的定义求出AT、BT,再根据正切的定义求出CT,结合图形计算,得到答案.
解:过B作BT⊥AC于T,
AB=1.5×34=51,
在Rt△ABT中,∠BAT=45°,
∴AT=BT=![]() ,
,
∠C=75°﹣45°=30°,
在Rt△CBT中,tanC=![]() ,
,
∴CT=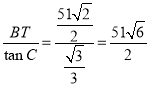 ,
,
∴AC=AT+CT=![]() ,
,
答:此时货轮与灯塔C的距离约为98海里.

练习册系列答案
 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目