题目内容
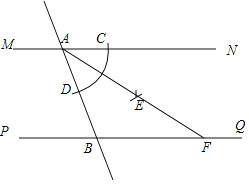
【题目】已知:如图,在△ABC中,AB=AC,BD平分∠ABC交AC于点D,DE平分∠ADB交AB于点E,过点C作CF∥AB交ED延长线于点F,若∠A=48°.
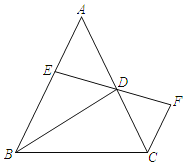
(1)求∠DBC的度数;
(2)求∠F的度数.
【答案】(1)33°;(2)82.5°
【解析】
(1)首先根据等腰三角形的性质得出∠ABC,然后根据角平分线的性质即可得出∠DBC;
(2)运用三角形内角和得出∠ADB,再根据角平分线性质得出∠ADE,进而得出∠AED,最后根据平行的性质得出∠F.
(1)∵AB=AC,∠A=48°.
∴∠ABC=66°,
∵BD平分∠ABC,
∴∠DBC=33°;
(2)∵∠DBC=33°,∠ACB=∠ABC=66°,
∴∠ADB=99°,
∵DE平分∠ADB,
∴∠ADE=49.5°,
∴∠AED=180°﹣49.5°﹣48°=82.5°,
∵CF∥AB,
∴∠F=∠AED=82.5°.

练习册系列答案
 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案
相关题目