Question

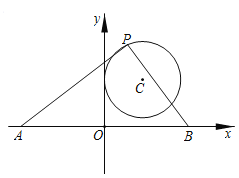
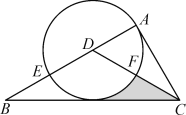
【题目】如图，在Rt△ABC中，∠BAC＝90°，CD平分∠ACB，交AB于点D，以点D为圆心，DA为半径的圆与AB相交于点E，与CD交于点F．

（1）求证：BC是⊙D的切线；

（2）若EF∥BC，且BC＝6，求图中阴影部分的面积．

Answer 1

【答案】（1）见解析；（2）－

【解析】

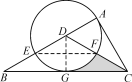
（1）过D作DG⊥BC于G，根据角平分线的性质得到DG=DA，根据切线的判定定理即可得到结论；
（2）连接EF，由已知和（1）的结论可得DG⊥EF，根据垂径定理、圆心角、弧之间的关系及等量代换可得∠CDG＝∠ADC＝∠BDG＝60°，再求出DG、CG的长，根据阴影部分的面积=△DGC的面积－扇形DGF的面积即可求解．

（1）过D作DG⊥BC于G，

∵DA⊥AC，∠ACD＝∠BCD，

∴DG＝DA，

∴BC是⊙D的切线．

（2）连接EF，

∵EF∥BC，由（1）DG⊥BC，

∴DG⊥EF，

∴，

∴∠EDG＝∠CDG．

由（1）∠ACD＝∠BCD，∠ACD＋∠ADC＝∠BCD＋∠CDG＝90°，

∴∠CDG＝∠ADC，

∴∠CDG＝∠ADC＝∠BDG＝60°．

∵EF∥BC，

∴∠DEF＝∠B， ∠DFE＝∠DCB，

在⊙D中，DE＝DF，

∴∠DFE＝∠DEF．

∴∠B＝∠DCB，

∴DB＝DC．

∵DG⊥BC，

∴CG＝BC＝3．

在Rt△DCG中，DG＝＝．

∴S阴影＝×3×－π()2＝－．