题目内容
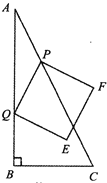
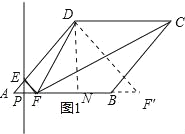
【题目】如图,在菱形ABCD中,∠DAB=45°,AB=2,P为线段AB上一动点,且不与点A重合,过点P作PE⊥AB交AD于点E,将∠A沿PE折叠,点A落在直线AB上点F处,连接DF、CF,当△CDF为等腰三角形时,AP的长是_____.
【答案】![]() 或1或1+
或1或1+![]() 或
或![]()
【解析】
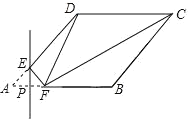
如图1,当DF=CD时,有一个解,如图2,当CF=CD=2时,有两个解,如图3中,当FD=FC时有一个解,根据折叠变换的性质和直角三角形的性质分别求出即可.
解:如图1,当DF=CD时,点F与A重合或在点F′处.
∵在菱形ABCD中,AB=2,
∴CD=AD=2,
作DN⊥AB于N,
由折叠的性质得:此时点P与N重合,
在Rt△ADN中,∵AD=2,∠DAN=45°,DN=AN=NF′=![]() ,
,
∴AP=![]() ;
;
如图2,当CF=CD=2时,点F与B重合或在F′处,
∵点F与B重合,
∴PE是AB的垂直平分线,
∴AP=![]() AB=1;
AB=1;
点F落在F'处时,AF'=2+2![]() ,
,
∴AP=![]() AF'=1+
AF'=1+![]() ;
;
如图3中,当FD=FC时,
AF=![]() +1,
+1,
∴AP=![]() AF=
AF=![]() .
.
综上所述:当△CDF为等腰三角形时,AP的长为![]() 或1或1+
或1或1+![]() 或
或![]() .
.
故答案为:![]() 或1或1+
或1或1+![]() 或
或![]()



练习册系列答案
相关题目