题目内容
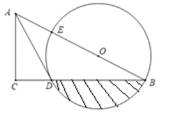
【题目】如图,已知⊙O的半径为5,弦AB,CD所对的圆心角分别是∠AOB,∠COD,下列说法正确的是( )①若∠AOB=∠COD,则CD=AB;②若CD=AB,则CD,AB所对的弧相等;③若CD=AB,则点O到CD,AB的距离相等;④若∠AOB+∠COD=180°,且CD=6,则AB=8.

A.①②③④B.①③④C.①②④D.③④
【答案】B
【解析】
①②根据圆心角、圆心角所对的弦、弧之间的关系即可判断;
③根据全等三角形的对应高相等判定即可;
④延长AO交⊙O于点E,连接BE,由∠AOB+∠BOE=∠AOB+∠COD知∠BOE=∠COD,据此可得BE=CD=6,在Rt△ABE中利用勾股定理求解可得.
若∠AOB=∠COD,则CD=AB,故①正确;
因为一条弦对两条弧,所以若CD=AB,则CD,AB所对的弧相等是错误的,故②错误;
若CD=AB,又OA=OC,OB=OD,则△OAB≌△OCD,则AB、CD边上的高相等,即则点O到CD,AB的距离相等,故③正确;
如图,延长AO交⊙O于点E,连接BE,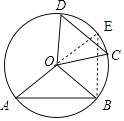
则∠AOB+∠BOE=180°,
又∵∠AOB+∠COD=180°,
∴∠BOE=∠COD,
∴BE=CD=6,
∵AE为⊙O的直径,
∴∠ABE=90°,
∴AB=![]()
故④正确.
故选:B

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目