题目内容
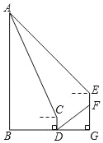
【题目】豆豆同学上周末对万州西山钟楼（AB）的高度进行了测量．如图，他站在点 D 处测得西山钟楼顶部点 A 的仰角为 67°．然后他从点 D 沿着坡度为 i=1:
的斜坡 DF 方向走 20 米到达点 F，此时测得建筑物顶部点 A 的仰角为 45°．已知该同学的视线距地面高度为 1.6 米（即 CD＝EF＝1.6 米），图 中所有的点均在同一平面内，点 B、D、G 在同一条直线上，点 E、F、G 在同一条直线上，AB、CD、EF 均垂直于 BG.则西山钟楼 AB 的高约为（ ）（参考数据：sin67°≈0.92，cos67°≈0.39，tan67°≈2.36）
A.17.4 米B.36.8 米C.48.8 米D.50.2 米
【答案】D
【解析】
在
中，根据坡度求出DG和FG，过E、C点作EH⊥AB，CK⊥AB，分别交AB于H，K.延长DC交HE于I.在
设AH=y米,则可求HE=y米.分别表示AK和KC，在
解直角三角形，求出y，随即可求出AB的长.
在中，
∵
，
∴
，
设FG=3x米,则DG=4x米
根据勾股定理
即
解得x=4或x=-4（舍去）
∴FG=3x=12米，DG=4x=16米.
如下图：过E、C点作EH⊥AB，CK⊥AB，分别交AB于H，K.延长DC交HE于I.
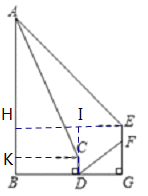
∵CK⊥AB
∴∠CKB=90°，
由题可得∠B=90°，∠CDB=90°，
∴四边形BDCK为矩形，
∴KB=CD=1.6米，CK=BD,
同理可证四边形HBGE为矩形
∴HB=EG，HE=BG，
∴HK=HB-KB=EF+GF-KB=GF=12米，
设AH=y米，
在中，
∵∠AEH=45°，
∴为等腰直角三角形，HE=AH=y米.
在中，AK=AH+HK=y+12米， CK=BD=BG-DG=y-16.
解得y≈36.6米
∴AB=AH+HB=36.6+12+1.6=50.2米.
故选D.
