题目内容
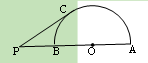
（11·柳州）如图，⊙O的半径为5，直径AB⊥CD，以B为圆心，BC长为半径作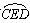
，则
围成的新月形ACED（阴影部分）的面积为_ ．
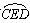，则围成的新月形ACED（阴影部分）的面积为_ ．72
连BC、BD，由直径AB⊥CD，根据圆周角定理和垂径定理得到△BCD为等腰直角三角形，
则BC=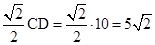
，新月形ACED（阴影部分）的面积=S半圆CD-S弓形CED，而S弓形CED=S扇形BCD-S△BCD，然后根据扇形的面积公式与三角形的面积公式进行计算即可．
解：连BC、BD，如图，
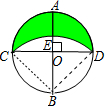
∵直径AB⊥CD，
∴△BCD为等腰直角三角形，
∴BC=，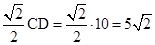
∴S弓形CED=S扇形BCD-S△BCD=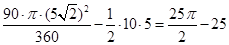
∴新月形ACED（阴影部分）的面积=S半圆CD-S弓形CED=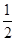
?π?52-（
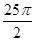-25）=25．
故答案为25．
则BC=
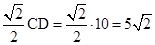，新月形ACED（阴影部分）的面积=S半圆CD-S弓形CED，而S弓形CED=S扇形BCD-S△BCD，然后根据扇形的面积公式与三角形的面积公式进行计算即可．解：连BC、BD，如图，
∵直径AB⊥CD，
∴△BCD为等腰直角三角形，
∴BC=
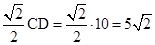，∴S弓形CED=S扇形BCD-S△BCD=
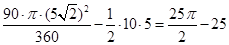
∴新月形ACED（阴影部分）的面积=S半圆CD-S弓形CED=
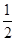?π?52-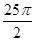（-25）=25．故答案为25．
练习册系列答案
相关题目
点D，过
AC＝60º时，DE与DF有何数量关系？请说明理由；
)，B(-2，0).
