题目内容
(10分)如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC于 点D,过
点D,过
点D作EF⊥AC于点E,交AB的延长线于点F.
(1)求证:EF是⊙O的切线;
(2)当∠B AC=60º时,DE与DF有何数量关系?请说明理由;
AC=60º时,DE与DF有何数量关系?请说明理由;
(3)当AB=5,BC=6时,求tan∠BAC的值.
 点D,过
点D,过点D作EF⊥AC于点E,交AB的延长线于点F.
(1)求证:EF是⊙O的切线;
(2)当∠B
 AC=60º时,DE与DF有何数量关系?请说明理由;
AC=60º时,DE与DF有何数量关系?请说明理由;(3)当AB=5,BC=6时,求tan∠BAC的值.


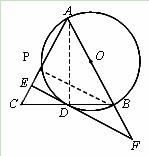
(1) 证明:连结OD,
∵AB=AC,∴∠2=∠C
又∵OD=OB,∴∠2=∠1
∴∠1=∠C
∴OD∥AC
∵EF⊥AC
∴OD⊥EF
∴EF是⊙O的切线。
(2)DE与DF的数量关系为:DF=2DE。理由如下:
连结
 AD
AD∵AB是⊙O的直径,∴AD⊥BC,
∵AB=AC。∴∠3=∠4=
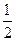 ∠BAC=30°
∠BAC=30°∵∠F=90°-∠BAC=90°-60°=30°, ∴∠3=∠F
∴AD=DF
∵∠4=30°,EF⊥AC,∴AD=2DE
∴DF=2DE.
(3)解:设⊙O与AC的交点为P,连结BP,则BP⊥AC,由上知BD=
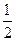 BC=3
BC=3∴
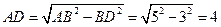
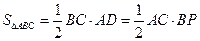
∴
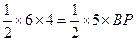
∴
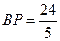
∴
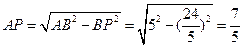
∴tan∠BAC=
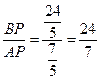
略

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目
 的直径,弦AC平分
的直径,弦AC平分 ,AD
,AD CD于D,BE
CD于D,BE
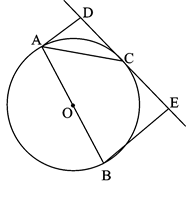
 ,边AD,DC都相切.把扇形BAE作一个圆锥的侧面,该圆锥的底面圆恰好是⊙O,则AD的长为( )
,边AD,DC都相切.把扇形BAE作一个圆锥的侧面,该圆锥的底面圆恰好是⊙O,则AD的长为( )





 ,则
,则 围成的新月形ACED(阴影部分)的面积为_ .
围成的新月形ACED(阴影部分)的面积为_ .
 长线上的一点,连接DC,且∠B=∠D=300。
长线上的一点,连接DC,且∠B=∠D=300。

 弦,OB=2,∠B=30°,
弦,OB=2,∠B=30°,