题目内容
【题目】如图,在平面直角坐标系中,坐标原点O是正方形OABC的一个顶点,已知点B坐标为(1,7),过点P(a,0)(a>0)作PE⊥x轴,与边OA交于点E(异于点O、A),将四边形ABCE沿CE翻折,点A′、B′分别是点A、B的对应点,若点A′恰好落在直线PE上,则a的值等于( )
A.![]() B.
B.![]() C.2D.3
C.2D.3
【答案】C
【解析】
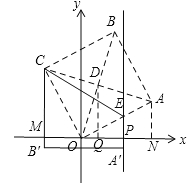
解:当点A′恰好落在直线PE上,如图所示,连接OB、AC交于点D,过点D、A作x轴的垂线,垂足分别为Q、N,设CB′交x轴于M,则CM∥QD∥AN.∵四边形OABC是正方形,∴OD=BD,OB⊥AC.∵O(0,0),B(1,7),∴D(![]() ,
,![]() ).由勾股定理得:OB=
).由勾股定理得:OB=![]() =
=![]() =
=![]() .∵△ABO是等腰直角三角形,∴AB=AO=5.∵DQ是梯形CMNA的中位线,∴CM+AN=2DQ=7.∵∠COA=90°,∴∠COM+∠AON=90°.∵∠CMO=90°,∴∠COM+∠MCO=90°,∴∠AON=∠MCO.∵四边形OABC是正方形,∴OA=OC.∵∠CMO=∠ONA=90°,∴△CMO≌△ONA,∴ON=CM,∴ON+AN=7.设AN=x,则ON=7﹣x.在Rt△AON中,由勾股定理得:x2+(7﹣x)2=52,解得:x=3或4.当x=4时,CM=3,此时点B在第二象限,不符合题意,∴x=3,∴OM=3.∵A′B′=PM=5,∴OP=a=2.故选C.
.∵△ABO是等腰直角三角形,∴AB=AO=5.∵DQ是梯形CMNA的中位线,∴CM+AN=2DQ=7.∵∠COA=90°,∴∠COM+∠AON=90°.∵∠CMO=90°,∴∠COM+∠MCO=90°,∴∠AON=∠MCO.∵四边形OABC是正方形,∴OA=OC.∵∠CMO=∠ONA=90°,∴△CMO≌△ONA,∴ON=CM,∴ON+AN=7.设AN=x,则ON=7﹣x.在Rt△AON中,由勾股定理得:x2+(7﹣x)2=52,解得:x=3或4.当x=4时,CM=3,此时点B在第二象限,不符合题意,∴x=3,∴OM=3.∵A′B′=PM=5,∴OP=a=2.故选C.

练习册系列答案
相关题目