Question

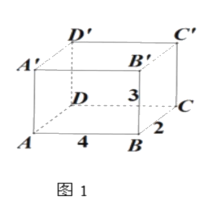
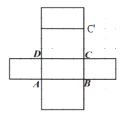
【题目】如图1是长方体模型，棱长如图所示，图2是它的一种表面展开图．

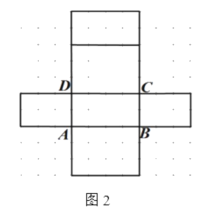
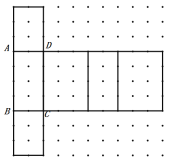
（1）①在图2中，表示出C可能的位置；

②在图3中画出长方体的一种展开图（不同于图2）；

（2）图1中，一只在顶点A的蚂蚁，要吃到C处的甜食，求它沿长方体表面爬行的最短距离；

（3） 在满足AB+BC+BB=9的条件下，当AB为何值时，蚂蚁从A沿长方体表面爬行到C距离最短，并写出其中的一种方案．

Answer 1

【答案】（1）①详见解析；②详见解析；（2）最短路径为；（3）AB=4.5时，蚂蚁从A沿长方体表面爬行到C距离最短

【解析】

（1）①根据长方体的平面展开图即可找到位置；

②根据题意画出正确的图形即可；

（2）连接AC′，求出AC′的长即可，分为三种情况：画出图形，根据勾股定理求出每种情况时AC′的长，再找出最短的即可；

（3）设AB=x，则BC′=，由勾股定理构建二次函数，根据二次函数的最值，即可求得答案．

（1）①C可能的位置如图所示：

②长方体的一种展开图如图所示：

（2）分为三种情况：
如图1，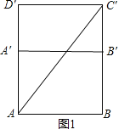

AB=4，BC′=3+2=5，
在Rt△ABC′中，由勾股定理得：

，

如图2，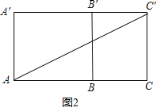

AC=4+2=6，CC′=3，
在Rt△ACC′中，由勾股定理得：

，

如图3，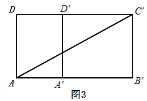

=3+4=7，C′=2，
在′中，由勾股定理得：

，

∴最短路径为；

（3）如图1：

设，则BC′=，

在Rt△ABC′中，由勾股定理得：

，

d=，

令y=2(x-)+，

∵且，

∴当时，，

∴当时，．

只要AB=4.5时，另外两棱和为4.5时，蚂蚁从A沿长方体表面爬行到C距离最短．