Question

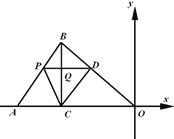
【题目】如图，顶点M在y轴上的抛物线与直线y=x+1相交于A、B两点，且点A在x轴上，点B的横坐标为2，连结AM、BM．

（1）求抛物线的函数关系式；

（2）判断△ABM的形状，并说明理由；

（3）把抛物线与直线y=x的交点称为抛物线的不动点．若将（1）中抛物线平移，使其顶点为（m，2m），当m满足什么条件时，平移后的抛物线总有不动点．

Answer 1

【答案】（1）抛物线解析式为y=x2﹣1；（2）△ABM为直角三角形．理由见解析；（3）当m≤时，平移后的抛物线总有不动点．

【解析】试题分析：（1）分别写出A、B的坐标，利用待定系数法求出抛物线的解析式即可；

根据OA＝OM＝1，AC＝BC＝3，分别得到∠MAC＝45°，∠BAC＝45°，得到∠BAM＝90°，进而得到△ABM是直角三角形；

（3）根据抛物线的平以后的顶点设其解析式为，

∵抛物线的不动点是抛物线与直线的交点，∴，

方程总有实数根，则≥0，得到m的取值范围即可

试题解析：解：（1）∵点A是直线与轴的交点，∴A点为（-1，0）

∵点B在直线上，且横坐标为2，∴B点为（2，3）

∵过点A、B的抛物线的顶点M在轴上，故设其解析式为：

∴，解得：

∴抛物线的解析式为．

（2）△ABM是直角三角形，且∠BAM＝90°．理由如下：

作BC⊥轴于点C，∵A（-1，0）、B（2，3）∴AC＝BC＝3，∴∠BAC＝45°；

点M是抛物线的顶点，∴M点为（0，-1）∴OA＝OM＝1，

∵∠AOM＝90°∴∠MAC＝45°；

∴∠BAM＝∠BAC＋∠MAC＝90°∴△ABM是直角三角形．

（3）将抛物线的顶点平移至点（， ），则其解析式为．

∵抛物线的不动点是抛物线与直线的交点，∴

化简得：

∴＝＝

当时，方程总有实数根，即平移后的抛物线总有不动点

∴．