题目内容
【题目】若等腰三角形的两边长为
和
，则它腰上的高长度为______．
【答案】
【解析】
先由三角形三边的关系判断出等腰三角形的三边长分别为8，8，4，再分别作出底边和腰上的高线，由勾股定理求出底边上的高，再由三角形等积式及可求解.
情况1：当等腰三角形的腰长为4时，则这个等腰三角形的三边长分别为4、4、8，
∵4+4=8，不满足三角形的三边关系，
∴此情况不存在等腰三角形；
情况2：当等腰三角形的腰长为8时，则这个等腰三角形的三边长分别为4、8、8，
∵4+8>8，8-4<8，符合三角形的三边关系，
∴此情况存在等腰三角形，
综上所述，这个等腰三角形的腰长为8，底边长为4.
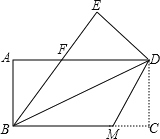
如图，
AB=AC=8，BC=4，过点A作AD
BC于点D，
∵AB=AC=8，AD⊥ BC，BC=8
∴BD=
BC=2（等腰三角形的三线合一）
由勾股定理得：AD=
，
过点C作CEAB于点E，
由
，得
，
即腰上的高为.
名校课堂系列答案【题目】数学活动课上，同学们探究了角平分线的作法．下面给出三个同学的作法：
小红的作法
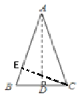
如图，∠AOB是一个任意角，在边OA、OB上分别取OM＝ON，再过点O作MN的垂线，垂足为P，则射线OP便是∠AOB的平分线．
小明的作法 如图，∠AOB是一个任意角，在边OA、OB上分别取OM=ON，移动角尺，使角尺两边相同的刻度分别与M，N重合，过角尺顶点C的射线OC便是∠AOB的平分线．
|
小刚的作法 如图，∠AOB是一个任意角，在边OA、OB上分别取OM＝ON，再分别过点M，N作OA，OB的垂线，交点为P，则射线OP便是∠AOB的平分线．
|
请根据以上情境，解决下列问题
(1)小红的作法依据是 ．
(2)为说明小明作法是正确的，请帮助他完成证明过程．
证明：∵OM＝ON，OC＝OC， ，
∴△OMC≌△ONC( )(填推理的依据)
(3)小刚的作法正确吗?请说明理由
