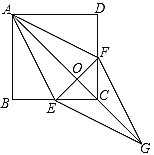
题目内容
【题目】如图,在平面直角坐标系中,点![]() ,
,![]() ,边
,边![]() 上有一点
上有一点![]() ,点
,点![]() ,
,![]() 分别在边
分别在边![]() ,
,![]() 上,联结
上,联结![]() ,
,![]() ,联结
,联结![]() ,
,![]() ,
,![]() .
.
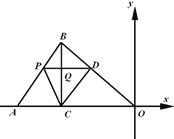
(1)求直线![]() 的解析式及点
的解析式及点![]() 的坐标;
的坐标;
(2当![]() 时,求出点
时,求出点![]() 的坐标;
的坐标;
(3)在(2)的条件下,点![]() 在射线
在射线![]() 上,
上,![]() ,请直接写出点
,请直接写出点![]() 的坐标.
的坐标.
【答案】(1)直线AB解析式为y=![]() x+9,P点坐标为(-
x+9,P点坐标为(-![]() ,2)(2)C点坐标为(-2,0)(3)R(2,-6).
,2)(2)C点坐标为(-2,0)(3)R(2,-6).
【解析】
(1)由A、B两点的坐标,利用待定系数法可求得直线AB的解析式,再把P点坐标代入直线解析式可求得P点坐标;
(2)由条件可证明△BPQ≌△CDQ,可证得四边形BDCP为平行四边形,由B、P的坐标可求得BP的长,则可求得CD的长,利用平行线分线段成比例可求得OC的长,则可求得C的坐标;
(3)由条件可知AR∥BO,故可先求出直线OB,BC的解析式,再根据直线平行求出AR的解析式,联立直线AR、BC即可求出R点坐标.
(1)设直线AB解析式为y=kx+b,
把A、B两点坐标代入可得![]() ,解得
,解得![]() ,
,
∴直线AB解析式为y=![]() x+9,
x+9,
∵![]() 在直线AB上,
在直线AB上,
∴2=![]() m+9,解得m=-
m+9,解得m=-![]() ,
,
∴P点坐标为(-![]() ,2);
,2);
(2)∵![]() ,
,
∴∠PBQ=∠DCQ,
在△PBQ和△DCQ中
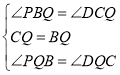

∴△PBQ≌△DCQ(ASA),
∴BP=CD,
∴四边形BDCP为平行四边形,
∵![]() ,(-
,(-![]() ,2),
,2),
∴CD=BP=![]() ,
,
∵A(-6,0),
∴OA=6,AB=![]() ,
,
∵CD∥AB,
∴△COD∽△AOB
∴![]() ,即
,即 ,解得CO=2,
,解得CO=2,
∴C点坐标为(-2,0);
(3)∵![]() ,
,
∴点A和点R到BO的距离相等,
∴BO∥AR,
设直线BO的解析式为y=nx,把![]() 代入得3=-4n,解得n=-
代入得3=-4n,解得n=-![]() x
x
∴直线BO的解析式为y=-![]() x,
x,
∴设直线AR的解析式为y=-![]() x+e,
x+e,
把A(-6,0)代入得0=-![]() ×(-6)+e
×(-6)+e
解得e=-![]()
∴直线AR的解析式为y=-![]() x-
x-![]() ,
,
设直线BC解析式为y=px+q,
把C、B两点坐标代入可得![]() ,解得
,解得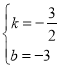 ,
,
∴直线AB解析式为y=-![]() x-3,
x-3,
联立
解得![]()
∴R(2,-6).

 阅读快车系列答案
阅读快车系列答案